Text size
Line height
Text spacing
Section outline
-
-
About the course
Uroš Lotrič, Davor Sluga, Timotej LazarUniversity of Ljubljana, Faculty of Computer and Information ScienceAt the workshop, we will get acquainted with the structure and software of computational clusters and start our first business. We will learn to distinguish between login nodes, master nodes, computation nodes, and data storage nodes. We will learn about the role of the operating system, Slurm middleware, environmental modules, containers and user applications. We will connect to login nodes, transfer files to and from the supercomputer, run transactions and monitor their implementation.The course of events
The workshop will take place in two afternoons. In the first meeting, we will get to know the hardware and software and in the second, we will use the supercomputer for video processing.Participants
The workshop is designed for researchers, engineers, students, and others who have realized that you need more computing resources than conventional computers can offer you.Acquired knowledge
After the workshop you will:- understand how a supercomputer works,
- know the main elements and their functions,
- know the Slurm middleware,
- understand environmental modules and containers,
- know how to work with files and do business,
- prepare execution scripts and
- process videos.
The material is published under license Attribution-NonCommercial-ShareAlike 4.0 International.
The workshop is prepared under the European project EuroCC, which aims to establish national centers of competence for supercomputing. More about the EuroCC project can be found on the SLING website.
-
-
-
The term supercomputer refers to the most powerful computer systems available at a given time. The most powerful systems in the world are published on top500.org. When working with supercomputers, we often talk about high-performance computing (HPC), as these are computer systems that are much more powerful than personal computers. Today's supercomputers consist of a multitude of computers or nodes interconnected by specially adapted networks for fast data transfer. Many nodes are additionally equipped with accelerators for certain types of calculations. Computer systems composed in this way are also referred to as a computer cluster.Supercomputers are designed for engineers, scientists, data analysts, and others who struggle with vast amounts of data or complex calculations that require billions of computational operations. They are used for computationally intensive calculations in various scientific fields such as biosciences (genomics, bioinformatics), chemistry (development of new compounds, molecular simulations), physics (particle physics, astrophysics), mechanical engineering (construction, fluid dynamics), meteorology, weather forecasting, climate studies), mathematics (cryptology) and computer science (law detection in data, artificial intelligence, image recognition, natural language processing).
Gaining access
Information about the procedure for obtaining access is usually published on the website of the supercomputer center. Computer systems under the auspices of SLING use the single sign-on system SLING SSO (Single Sign-On). More details can be found on the pages of SLING and the HPC-RIVR project.Login nodes
During our course we will start operations on the supercomputer via Slurm middleware. The computer clusters within the open access that allow working with the Slurm system are NSC, Maister and Trdina. To work with the Slurm system, we connect to the computer cluster via the login node. Names of login nodes on the mentioned clusters:A computer cluster consists of a multitude of nodes fairly closely connected to a network. Nodes work in the same way and consist of the same elements as found in personal computers: processors, memory, and input / output units. Clusters, of course, predominate in the quantity, performance, and quality of the built-in elements, but they usually do not have input-output devices such as a keyboard, mouse, and screen.
Node types
We distinguish several types of nodes in clusters, their structure depends on their role in the system. The following are important for the user:
- head nodes,
- login nodes,
- compute nodes and
- data nodes.
The main node ensures the coordinated operation of the entire cluster. It runs programs that monitor the status of other nodes, classify transactions into computational nodes, control the execution of transactions and more.Users log in to the login node using software tools via the SSH protocol. Through the login node, we transfer data and programs to and from the cluster, prepare, monitor and manage transactions for computing nodes, reserve computing time at computing nodes, log in to computing nodes etc.The tasks that we prepare at the login node are performed at the computational nodes. We distinguish several types of computational nodes. In addition to the usual processor nodes, we have more powerful nodes with more memory and nodes with accelerators, such as general-purpose graphics processing units. Computational nodes can be grouped into groups or partitions.We store data and programs on data nodes. Data nodes are connected to a distributed file system (for example, ceph). The distributed file system is seen by all login and array nodes. Files that are transferred via the login node to the cluster are stored in a distributed file system.All nodes are interconnected by high-speed network connections, usually including an Ethernet network and sometimes an Infiniband (IB) network for efficient communication between computing nodes. For network connections, it is desirable that they have high bandwidth (the ability to transfer large amounts of data) and low latency (they need a short time to establish a connection).Node structure
The vast majority of computers today follow Von Neumann’s architecture. In the processor, the control unit takes care of the coordinated operation of the system, reads commands and operands from memory and writes the results to memory. The processor executes commands in the arithmetic logic unit (ALE), using registers (for example, tracking program flow, storing intermediate results). Memory stores data - commands and operands, and input-output units transfer data between the processor and memory and the outside world.Graphic processing units
Some nodes are additionally equipped with calculation accelerators. Today, graphics processing units are mostly used as accelerators. The basic task of graphics cards is to relieve the processor when drawing graphics on the screen. When plotting on a screen, they have to perform a multitude of independent calculations for millions of screen points. When they are not plotting on the screen, however, they can only count.We are talking about General Purpose Graphics Porcessing Units (GPGPU). They cut perfectly whenever we have to do a multitude of similar calculations on a large amount of data with few dependencies. For example, in deep learning in artificial intelligence and in video processing. The architecture of graphics processing units is quite different from the architecture of conventional processors. Therefore, in order to effectively implement programs on graphics processing units, we need to heavily rework existing programs.Computer cluster software consists of:
- operating system,
- middleware and
- user software (applications).
Operating system
An operating system is a bridge between user software and computer hardware. It is software that performs basic tasks such as: memory management, processor management, device control, file system management, implementation of security functions, system operation control, resource consumption monitoring, error detection. Popular operating systems are free Linux, paid macOS and Windows. The CentOS Linux operating system is installed on the nodes of the NSC, Maister, and Trdina clusters.
Intermediate software
Middleware is software that clusters the operating system and user applications. In the computer cluster, it takes care of the coordinated operation of a multitude of nodes, enables centralized management of nodes, takes care of user authentication, controls the execution of transactions (user applications) on nodes and the like. Users of computer clusters mostly work with middleware for business monitoring, and SLURM (Simple Linux Utility for Resource Management) is very widespread. The Slurm system manages the queue, allocates the required resources to the business and monitors the execution of business. With the Slurm system, users provide access to resources (computing nodes) for a certain period of time, start transactions and monitor their implementation.
User software
User software is the key software that makes us use computers, both regular and computer clusters. With the user software, users perform the desired functions. Only user software adapted for the Linux operating system can be used on clusters. Some examples of user software used on clusters: Gromacs for molecular dynamics simulations, OpenFOAM for fluid flow simulations, Athena collision analysis software on the LHC collider at CERN (ATLAS), TensorFlow for learning deep models in artificial intelligence. In the workshop, we will use the FFmpeg video processing tool.
User software can be clustered in a variety of ways:
- the administrator installs it directly on the nodes,
- the administrator prepares environmental modules,
- the administrator prepares containers for general use,
- the user places it in his folder, the user prepares the container in his folder.
To make system maintenance easier, administrators install the user software in the form of environmental modules, preferably in the form of containers.
Environmental modules
When logging in to the cluster, we find ourselves in the command line with the standard environment settings. This environment can be supplemented for easier work, most simply with environmental modules. Environmental modules are a tool for changing command line settings and allow users to easily change the environment while working.
Each environment module file contains the information needed to set the command line for the selected software. When we load the environment module, we adjust the environment variables to run the selected user software. One such variable is PATH, which lists the folders where the operating system searches for programs.
The environmental modules are installed and updated by the cluster administrator. By preparing environmental modules for the software, it facilitates maintenance, avoids installation problems due to the use of different versions of libraries, and the like. The prepared modules can be loaded and removed by the user during work.
Virtualization and containers
As we have seen, we have a multitude of processor cores on nodes that can run a multitude of user applications simultaneously. When installing user applications directly on the operating system, it can get stuck, mostly due to improper versions of libraries.
Node virtualization is an elegant solution that ensures the coexistence of a wide variety of user applications and therefore easier system management. The capacity of the system is slightly lower due to virtualization, of course at the expense of greater robustness and ease of system maintenance. We distinguish between hardware virtualization and operating system virtualization. In the first case we are talking about virtual machines (virtual machines), in the second about containers (containers).
Container virtualization is more suitable for supercomputer clusters. The containers do not include the operating system, so they are smaller and it is easier for the controller to switch between them. The container supervisor keeps the containers isolated from each other and gives each container access to a common operating system and core libraries. Only the necessary user software and additional libraries are then installed separately in each container.
Computer cluster administrators want users to use containers as much as possible, because:- we can prepare the containers ourselves (we have the right to install the software in the containers),
- containers offer us many options for customizing the operating system, tools and user software,
- containers ensure repeatability of business execution (same results after upgrading the operating system),
- through containers, administrators can more easily control resource consumption.
Docker containers are the most common. On the mentioned clusters, a Singularity controller is installed for working with containers, which is more adapted for work in a supercomputer environment. In the Singularity container environment, we can work with the same user account as on the operating system, we have organized access to the network and data. The Singularity monitor can run Docker and other containers.
-
-
Dear hackathon attendee,
on Day 2 of the hackathon we will open a survey to get your feedback about the event. The survey is a standard ELIXIR short-term feedback survey and its results will be uploaded to the ELIXIR Training Metrics Database. The survey is anonymous. -
-
Parallel video processing
Many problems can be broken down into independent subproblems that can be processed in a parallel manner. A common phrase for this is: embarrassingly parallel problems.
One such problem is video processing. Here's how to speed up video processing:
- first divide the video into a multitude of pieces on one core,
- then each piece is processed separately on its core and
- at the end the processed pieces are assembled back into a whole.
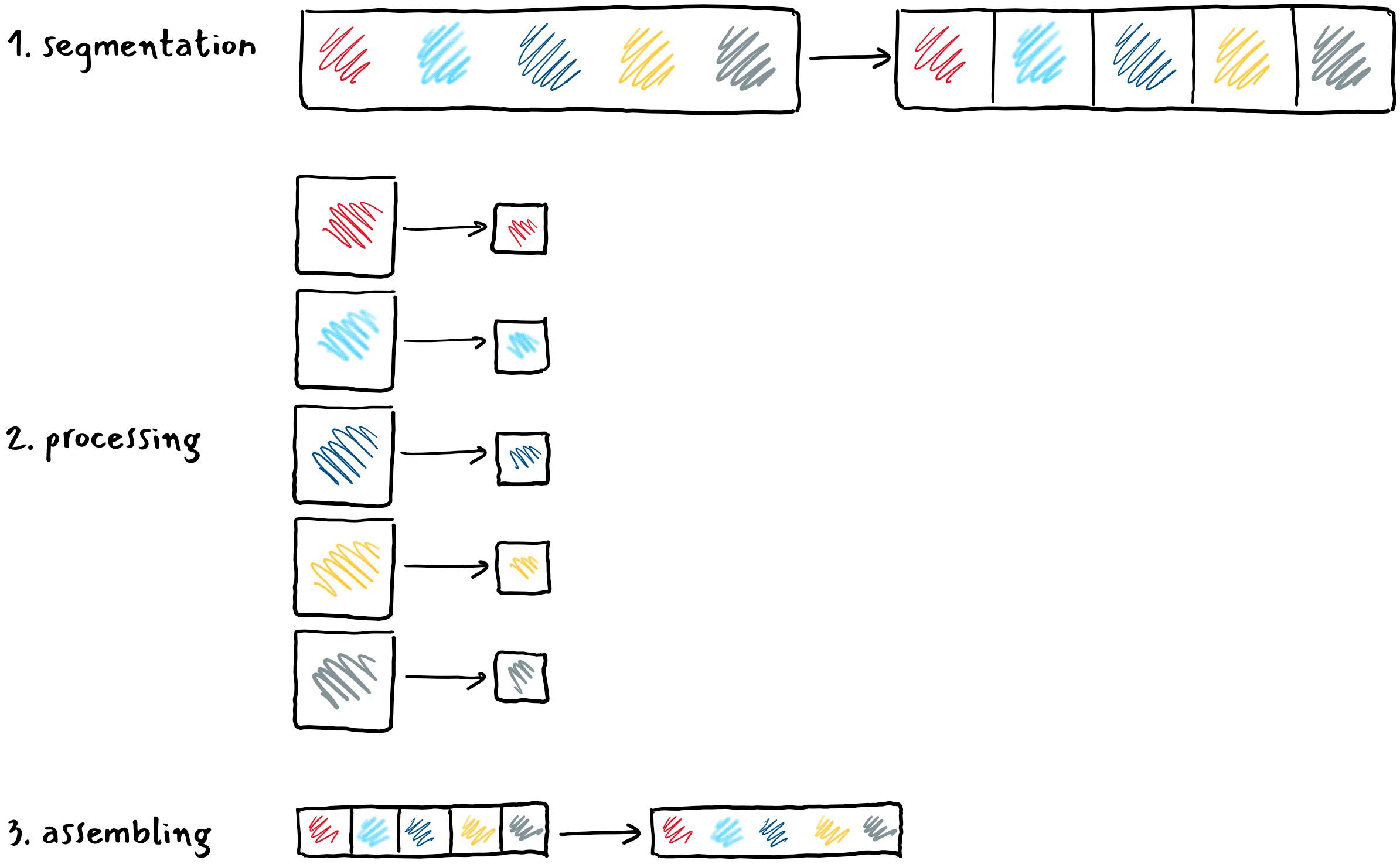The advantage of such an approach is that the individual pieces are processed in a parallel manner, each at its own core. If we divided the video into N equal pieces in the first step, the processing time in the second step is approximately equal to the N part of the time required to process the entire video on one core. Even if we take into account the steps of cutting and assembling at the time of processing, which we do not have when processing on one core, we can still gain a lot in the end.
First, download the videobbb.mp41to the cluster.Step 1: Segmentation
We want to break the bbb.mp4 video into smaller pieces, which we will then process in a parallel manner. First we load the appropriate module, if we haven't already.We then divide the video into pieces that are 130 seconds long with the following command:where:
- -codec copy tells the audio and video to be copied unchanged to the output files,
- -f segment selects a segmentation option that cuts the input file,
- -segment_time 130 specifies the desired duration of each piece in seconds,
- -segment_list parts.txt saves the list of created pieces in the parts.txt file,
- part-%d.mp4 specifies the name of the output files, where %d is the extension that ffmpeg replaces with the sequence number of the piece during partitioning.
When the process is complete, we have the original video in the working directory, a list of parts.txt pieces, and sequential pieces part-0.mp4 to part-4.mp4:Step 2: Processing
We process each piece in the same way. For example, if you want to reduce the dimensions of a part-0.mp4 piece by half and save the result to an out-part-0.mp4 file, use the command from the previous section:As always, the srun will require resources and run our task on the assigned computing node. In this way, we could process all the pieces one by one, but with a lot of manual work. So let’s take a look at a simple sbatch script that does this for us.#!/bin/sh
#SBATCH --job-name=ffmpeg1 # job name
#SBATCH --output=ffmpeg1.txt # execution log file
#SBATCH --time=00:10:00 # time limit for running job hours: minutes: seconds
#SBATCH --reservation=fri # reservation, if any; otherwise we delete the line
srun ffmpeg -y -i part-0.mp4 -codec:a copy -filter:v scale=w=iw/2:h=ih/2 out-part-0.mp4
srun ffmpeg -y -i part-1.mp4 -codec:a copy -filter:v scale=w=iw/2:h=ih/2 out-part-1.mp4
srun ffmpeg -y -i part-2.mp4 -codec:a copy -filter:v scale=w=iw/2:h=ih/2 out-part-2.mp4
srun ffmpeg -y -i part-3.mp4 -codec:a copy -filter:v scale=w=iw/2:h=ih/2 out-part-3.mp4
srun ffmpeg -y -i part-4.mp4 -codec:a copy -filter:v scale=w=iw/2:h=ih/2 out-part-4.mp4Save the script to the file ffmpeg1.sh and run it with the commandSo far, we haven't sped up the execution, as the script waits for each srun call to finish before running the next one. If we want to send all the pieces for processing at the same time, we add an & character at the end of each srun line, requiring the command to run in the background. Now the script does not wait for the command to complete, but immediately resumes executing the next command. At the end of the script, we must therefore add the wait command, which waits for all the tasks we ran in the background to complete. This makes sure that the script is not completed until all the pieces of video have been processed to completion.Each srun call represents one task in our job. Therefore, in the header of the script, we ask how many tasks to perform at a time. The setting --ntasks=5 means that Slurm will perform a maximum of five tasks at a time, even if there are multiple tasks. Be careful to add the argument --ntasks=1 to each srun call; without it, Slurm would repeat the task for each piece five times, which is not the most useful.#!/bin/sh
#SBATCH --job-name=ffmpeg2
#SBATCH --output=ffmpeg2.txt
#SBATCH --time=00:10:00
#SBATCH --ntasks=5 # the number of tasks in the job that are performed simultaneously
srun --ntasks=1 ffmpeg -y -i part-0.mp4 -codec:a copy -filter:v scale=w=iw/2:h=ih/2 out-part-0.mp4 &
srun --ntasks=1 ffmpeg -y -i part-1.mp4 -codec:a copy -filter:v scale=w=iw/2:h=ih/2 out-part-1.mp4 &
srun --ntasks=1 ffmpeg -y -i part-2.mp4 -codec:a copy -filter:v scale=w=iw/2:h=ih/2 out-part-2.mp4 &
srun --ntasks=1 ffmpeg -y -i part-3.mp4 -codec:a copy -filter:v scale=w=iw/2:h=ih/2 out-part-3.mp4 &
srun --ntasks=1 ffmpeg -y -i part-4.mp4 -codec:a copy -filter:v scale=w=iw/2:h=ih/2 out-part-4.mp4 &
waitArray jobs
The above method works, but is quite inconvenient. If we change the number of pieces, we need to add or correct lines in the script, which can quickly go wrong. We also see that the individual steps differ from each other only in number in the file names. Fortunately, Slurm has a solution for just such situations: array jobs. Let's look at how to process the above example:#!/bin/sh
#SBATCH --job-name=ffmpeg3
#SBATCH --time=00:10:00
#SBATCH --output=ffmpeg3-%a.txt # %a je nastavek za oznako naloge
#SBATCH --array=0-4 # območje spreminjanja vrednosti
srun ffmpeg \
-y -i part-$SLURM_ARRAY_TASK_ID.mp4 -codec:a copy -filter:v scale=w=iw/2:h=ih/2 \
out-part-$SLURM_ARRAY_TASK_ID.mp4We've added a switch --array=0-4, which tells Slurm to run the commands in the script for each of the numbers 0 through 4. Slurm will run as many tasks as there are numbers in the range specified by the --array switch in our case 5. If we want to limit the number of tasks performed simultaneously, for example to 3, we write --array=0-4%3.
Each srun command will be executed for one task, so --ntasks=1 can be omitted. We do not specify the actual file name in the command, but use the $SLURM_ARRAY_TASK_ID extension. For each task, Slurm will replace the attachment with one of the numbers from the range specified by the --array switch. We added the %a extension to the log file name, which Slurm also replaces with a number from the range specified by the --array switch. This will write each task to its own file. The $SLURM_ARRAY_TASK_ID is essentially an environmental variable that Slurm sets accordingly for each task. When Slurm executes the #SBATCH commands, this variable does not yet exist, so we must use the %a extension for the switches in Slurm.
After this step, we get out-part-0.mp4 to out-part-4.mp4 files in the working directory with the processed pieces of the original clip.Step 3: Assembling
All we have to do is combine the out-part-0.mp4 … out-part-4.mp4 files into one clip. To do this, we need to give ffmpeg a list of the pieces we want to merge. We list them in the out-parts.txt file with the following content:file out-part-0.mp4
file out-part-1.mp4
file out-part-2.mp4
file out-part-3.mp4
file out-part-4.mp4It can be created from the existing list of pieces of the original parts.txt clip. First rename the file to out-parts.txt. Open the out-parts.txt file in a text editor and find and replace all part strings with the file out-part string.
More elegantly, we can create a list of individual pieces of video with the help of the command line and the program sed (stream editor):Finally, from the list of pieces in the file out-parts.txt, we compose the output clip out-bbb.mp4.Finally, we can use the data transfer tool to remove temporary files.Steps 1, 2, 3 in one go
In previous sections, we speeded up video processing by dividing the task into several pieces, which we performed as multiple parallel tasks. We ran ffmpeg over each piece, each task used one kernel and knew nothing about the remaining pieces. Such an approach can be taken whenever the problem can be divided into independent pieces. We do not need to change the processing program.
In principle, each business is limited to one processor core. However, using program threads, one job can use multiple cores. The ffmpeg program can use threads for many operations. The above three steps of peeling can also be performed with a single command. We now run the job with a single task for the whole file, as the ffmpeg program will divide the processing into several pieces according to the number of cores we assign to it.So far, we have done all the steps using the FFmpeg module. This time we use the ffmpeg-alpine.sif container. If we haven't already, we transfer the FFmpeg container from the link to the cluster. When using the container before calling ffmpeg, add singularity exec ffmpeg_alpine.sif. Three programs are now included in the command:- srun sends the business to Slurm and starts the singularity program,
- the singularity program starts the ffmpeg-alpine.sif container and
- inside the ffmpeg-alpine.sif container it starts the ffmpeg program.
The process we used to do ourselves in three steps is now done by ffmpeg in about the same amount of time. With the --cpus-per-task switch we requested that Slurm reserve 5 processor cores for each task in our business.While working, ffmpeg displays the status in the last line:frame=17717 fps=125 q=29.0 size= 48128kB time=00:09:50.48 bitrate= 665.7kbits/s speed=4.16xThe speed data tells us that encoding is 4.06 times faster than real-time playback. In other words, if the video lasts 10 minutes, we will spend 10.5/4.16≈2.5 minutes encoding.
-
-
Heterogeneous systems
A heterogeneous computer system is a system that, in addition to the classic central processing unit (CPU) and memory, also contains one or more different accelerators. Accelerators are computing units that have their own process elements and their own memory, and are connected to the central processing unit and main memory via a fast bus. A computer that contains accelerators in addition to the CPU and main memory is called a host. The figure below shows an example of a general heterogeneous system.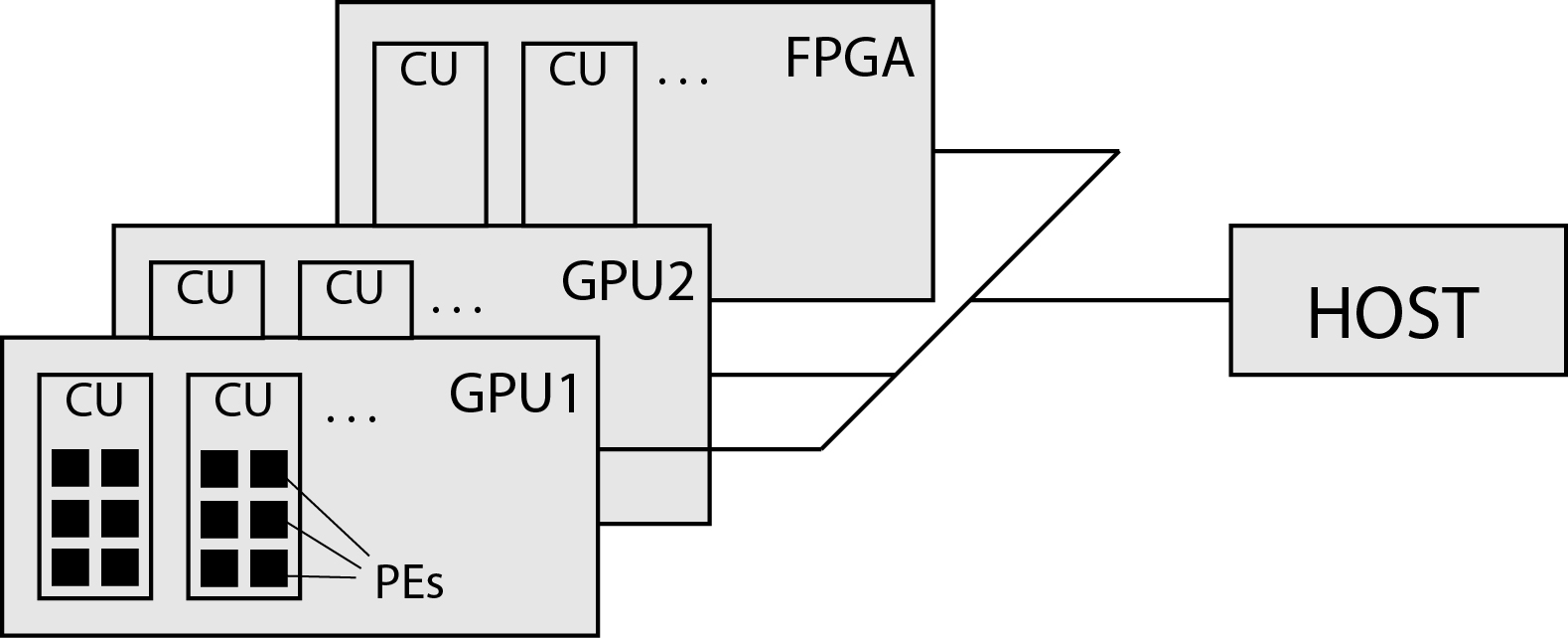
Today we know a series of accelerators. The most widely used are graphics processing units (GPUs) and programmable field arrays (FPGAs). Accelerators have a large number of dedicated process units and their own dedicated memory. Their process units are usually adapted to specific problems (for example, performing a large number of matrix multiplications) and can perform these problems fairly quickly (certainly much faster than a CPU). We call an accelerator a device.
Devices process data in their memory (and their address space) and in principle do not have direct access to the main memory on the host. On the other hand, the host can access the memories on the accelerators, but cannot address them directly. It accesses the memories only through special interfaces that transfer data via the bus between the device memory and the main memory of the host.
The figure below shows the organization of a smaller heterogeneous system such as that found in a personal computer. The host is a personal desktop computer with an Intel i7 processor.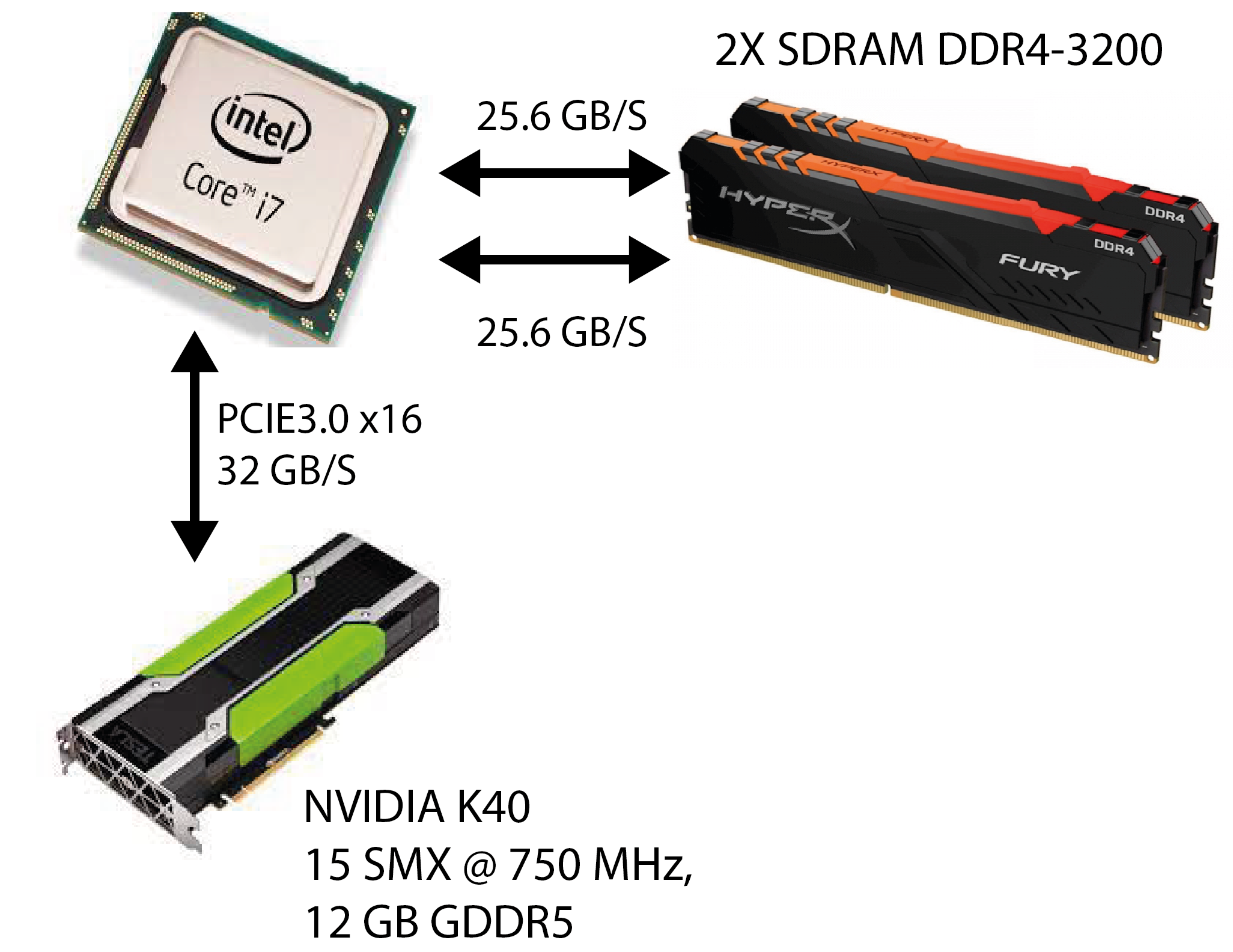
The main memory of the host is in DDR4 DIMMs and is connected to the CPU via a memory controller and a two-channel bus. The CPU can address this memory (for example, with LOAD / STORE commands) and store commands and data in it. The maximum theoretical single channel transfer rate between the DIMM and the CPU is 25.6 GB / s. The accelerator in this heterogeneous system is the Nvidia K40 graphics processing unit. It has a large number of process units (we will get to know them below) and its own memory (in this case it has 12 GB of GDDR5 memory). Memory in the GPE can be addressed by process units in the GPE, but cannot be addressed by the CPU on the host. Also, processors on the GPE cannot address the main memory on the host. The GPE (device) is connected to the CPU (host) via a high-speed 16-channel PCIe 3.0 bus, which enables data transfer at a maximum of 32 GB / s. Data between the main memory on the host and the GPE memory can only be transferred by the CPU via special interfaces.Programming of heterogeneous systems
We will use the OpenCL framework to program heterogeneous computer systems. Programs written in the OpenCL framework consist of two parts:- program to be run on the host and
- program running on the device (accelerator).
A host program
The program on the host will be written in the C programming language as part of the workshop. It is an ordinary program contained in the C function main(). The task of the program on the host is to:- determine what devices are in the system,
- prepare the necessary data structures for the selected device,
- create buffers to transfer data to and from the device
- reads and translates from a file the program that will run on the device,
- the translated program downloads along with the data to the device and runs it,
- after the program runs on the device, it transfers the data back to the host.
Program on the device
We will write programs for devices in the OpenCL C language. We will learn that this is actually a C language with some changed functionalities. Programs written for the device are first translated on the host, then the host, along with the data and arguments, transfers them to the device where they are executed. The program running on the device is called a kernel. Pliers are run in parallel - a large number of process units on the device are run by the same kernel. In the following, we will get to know the implementation model provided for the devices by the OpenCL framework. The OpenCL framework provides the same runtime model and the same memory hierarchy for all types of devices, so we can program very different devices with it. In the workshop, we will limit ourselves to programming graphic process units. -
Anatomy of graphic process units
To make it easier to understand the operation and structure of modern graphic units, we will look below at a simplified description of the idea that led to their emergence. GPUs were created in the desire to execute program code which has a large number of relatively simple and repetitive operations on a large number of smaller processing units and not on a large, complex and energy-hungry central processing unit. Many of the problems that modern GPUs are designed for include: image and video processing, operations on large vectors and matrices, deep learning, etc.
Modern CPUs are very complex digital circuits that speculatively execute commands in multiple pipelines, and the commands support a large number of diverse operations (more or less complex). CPUs have built-in branch prediction units and trace types in the pipelines, in which they store microcodes of commands waiting to be executed. Modern CPUs have multiple cores and each core has at least a first-tier L1 cache. Due to the above, the cores of modern CPUs together with caches occupy a lot of space on the chip and consume a lot of energy. In parallel computing, we strive to have as many simple process units as possible that are small and energy efficient. These smaller processing units typically operate at a clock speed several times lower than the CPU clock clock. Therefore, smaller process units require a lower supply voltage and thus significantly reduce energy consumption.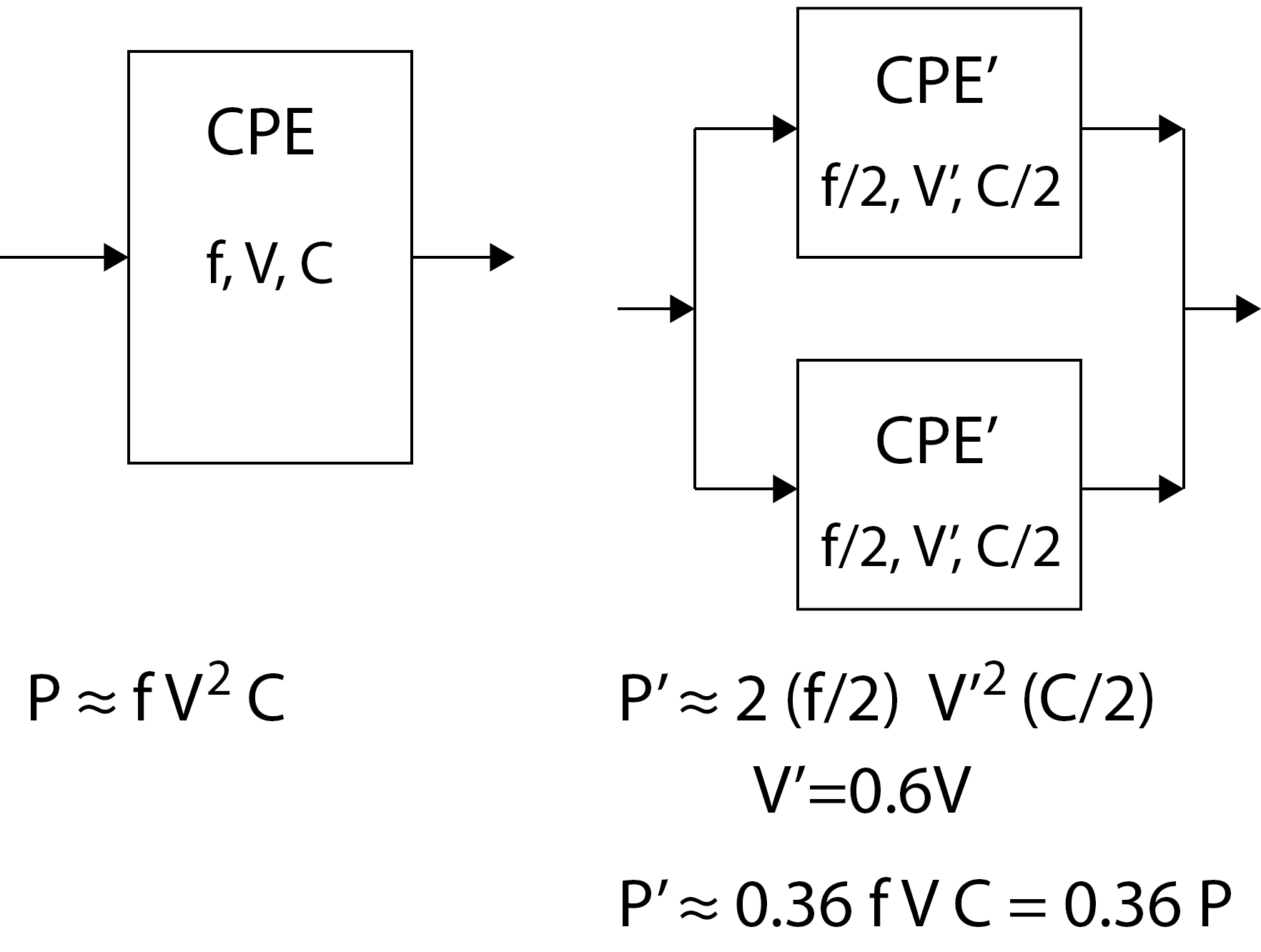
The figure above shows how power and power consumption can be reduced in a parallel system. On the left side of the image is a CPU that processes with frequency f. To work with frequency f, it needs the energy it gets from the supply voltage V. The internal capacitance (that is, a kind of inertia that resists rapid voltage changes on digital connectors) of such a CPU depends mainly on its size on the chip and is marked with C. The power required by the CPU for its operation is proportional to the clock frequency, the square of the supply voltage and the capacitance.
On the right side of the image, the same problem is solved with two CPU' processing units connected in parallel. Suppose that our problem can be broken down into two exactly the same subproblems, which we can solve separately, each on its own CPU'. Assume also that the CPUs' processing units are half the size of the CPU in terms of chip size and that they operate at a frequency of f/2. Because they work at half frequency, they also need less energy. It turns out that if we halve the clock frequency in a digital system, we only need 60% of the supply voltage for the system to work. As the CPUs are half as small, their capacitance is only C/2. The power P' that such a parallel system now needs for its operation is only 0.36 P.The evolution of GPU
Suppose that we want to add two vectors vecA and vecB with the function vectorAdd() in C and save the result in the vector vecC. All vectors are of length 128.void vectorAdd( float *vecA, float *vecB, float *vecC ) { int tid = 0; while (tid < 128) { vecC[tid] = vecA[tid] + vecB[tid]; tid += 1; } }In the code above, we intentionally used the while loop, in which we sum all the output elements of the vectors. The index of the current element was intentionally written with a tid, which is an abbreviation of thread index. Why we chose just such a name, we find out below.Execution on one CPU
Let's suppoes we want to run the vectorAdd() function on one simple CPU, which is shown in the figure below. The CPU has logic for capturing and decoding commands, an arithmetic-logic unit, and a set of registers containing operands for the arithmetic-logic unit.
In addition to the CPU, the pseudo-collection code of the vectorAdd() function is shown in the figure above. We won’t go into its details, let’s just point out that the code in loop L1 is repeated 128 times.Execution on two CPUs
Now let's suppose we want to run the vectorAdd() function on two identical CPUs as before. The figure below shows the two CPUs and the pseudo-compiler codes running on each of these two CPUs. Again, we won’t go into the details of the collection code. Note only that the code in the L1 loop is repeated only 64 times this time, as each CPU this time adds only half of the identical elements in the vectors (the left CPU adds the first 64 elements, while the right CPU adds the last 64 elements). We can estimate that the implementation of the vectorAdd() function has been accelerated twice. We also say that two parallel threads are now running on two CPUs at the same time.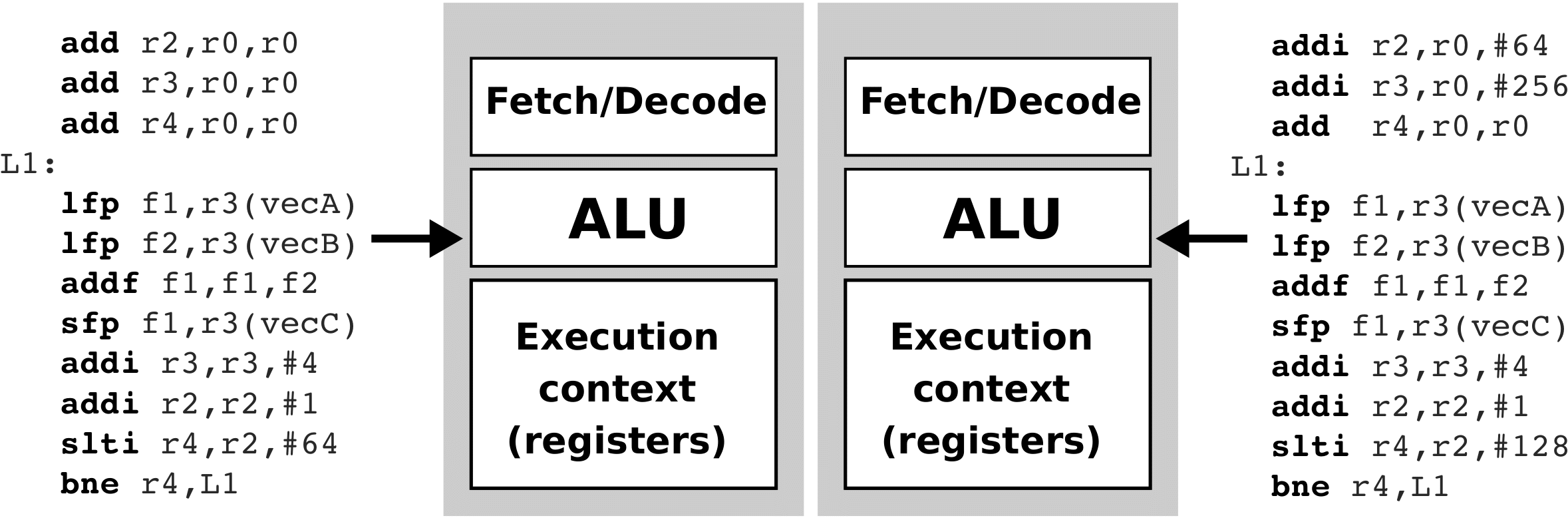
Compute unit and process elements
Let's suppose now that the upper CPU is expanded so that instead of a single arithmetic-logic unit it has eight arithmetic logic units. In addition, we add eight register strings to it, so that each arithmetic-logic unit can have its own set of registers in which to store its operands. In this way, arithmetic-logic units can calculate simultaneously, independently of each other! So, instead of replicating the entire CPU eight times, this time we only replicated its arithmetic-logic units and register string eight times. Such a CPU is shown in the figure below.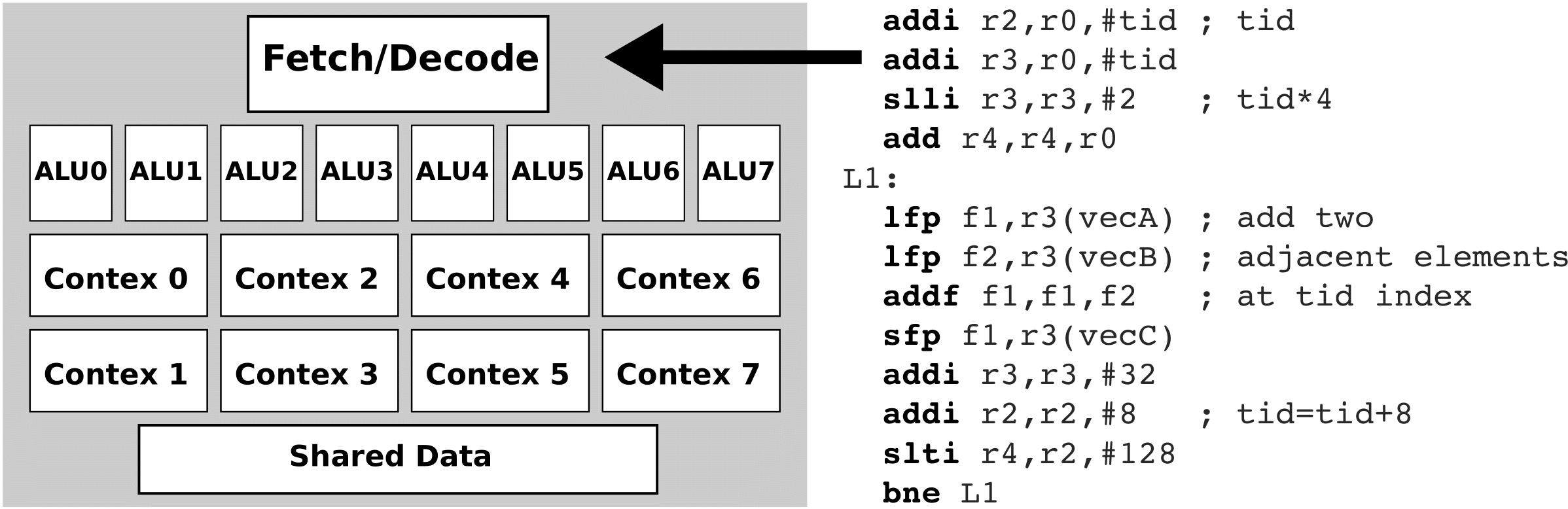
Note, however, that such a CPU still has only one unit for capturing and decoding commands - this means that it can only take over and decode one command in one clock cycle! Therefore, such a CPU will issue the same execution command to all arithmetic-logic units. However, this time the operands in the command can be vectors of length 8. This means that we will now be able to add 8 identical elements in the vector in one cycle (simultaneously) and repeat the loop only 16 times. Such a processing unit will be called a compute unit (CU). A compute unit can execute a single command over a large amount of data - in fact, in our case, a compute unit will add eight identical vector elements with just one command to read and decode. This method of implementation is called SIMD (Single Instruction Multiple Data). Because the compute unit executes each command in eight arithmetic-logic units, it looks as if different threads of the same command string are executed in arithmetic-logic units over different data. Therefore, such an implementation is also called SIMT (Single Instruction Multiple Threads). Arithmetic-logic units that execute the same command over different operands are called processing elements (PE). The figure below shows the SIMD (SIMT) execution of commands.
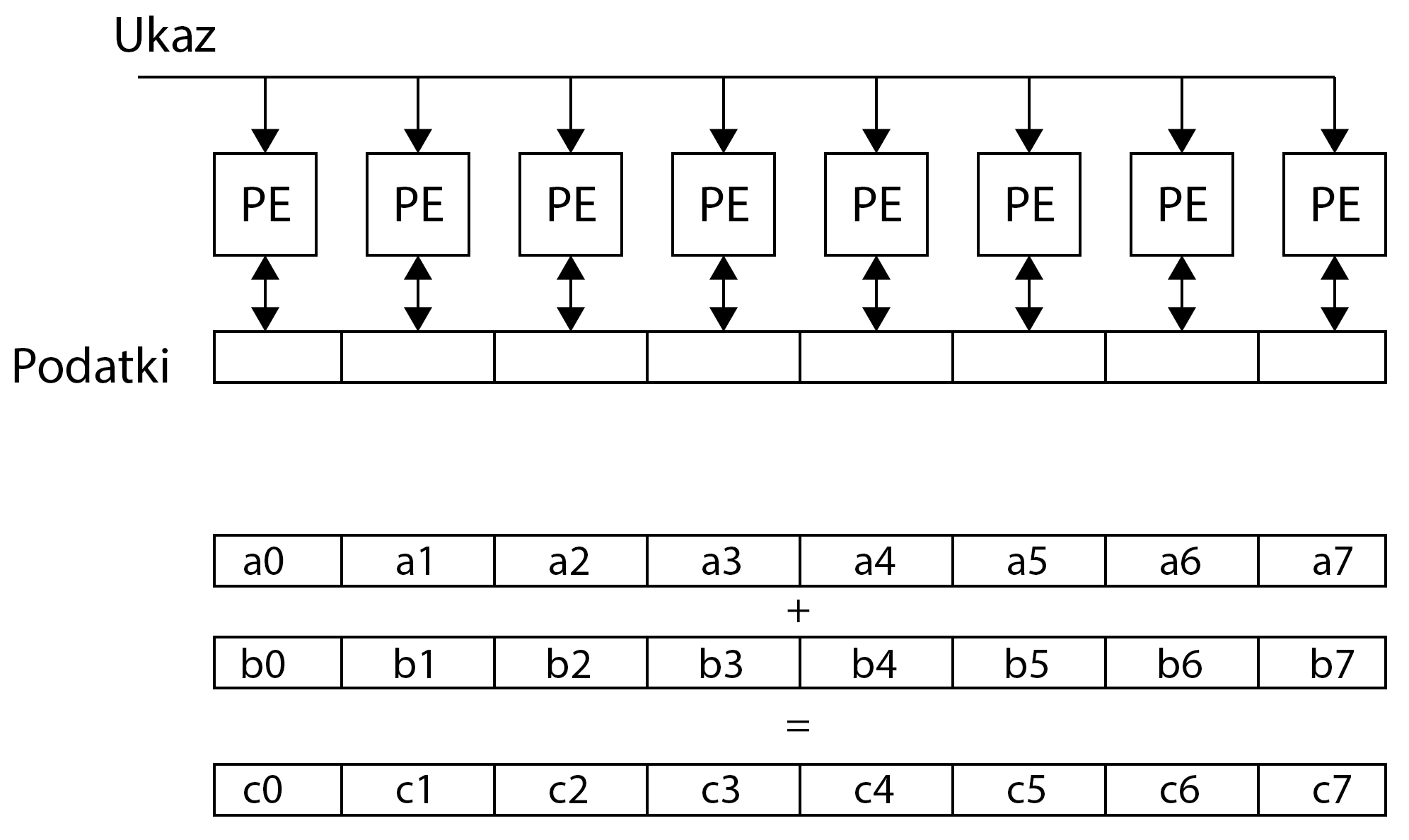The registers in the process elements are usually private for each process element separately, which means that other process elements cannot access the data in the registers. through which they can even share data. The L1 loop is repeated only 16 times this time!Graphic processing unit
Let's take it one step further. Instead of one calculation unit in the system, we use as many as 16 calculation units, as shown in the figure below.
Now we do not have to repeat the loop 16 times but assign only one iteration of the loop to each compute unit. The figure above shows a simplified structure of graphic processing units.Summary
Graphic processing units consist of a large number of mutually independent compute units. Compute units consist of a large number of processing elements. In a slightly simplified way, we can assume that all compute units, hereinafter referred to as CUs, execute the same program (kernel), and the process elements (PE) within one CU execute the same commands at the same time. In doing so, different CUs may perform different parts of the tongs at some point. We also say that compute units execute groups of threads, and process elements execute individual threads.
-
-
-
Nvidia Tesla K40 GPE
Let's look at the structure of a typical GPU on the example of Nvidia Tesla K40, shown in the picture below. It contains 15 compute units (CU), which Nvidia calls the NeXt Generation Streaming Multiprocessor (SMX).
The CU structure is shown in the figure below. It contains 128 processors, which Nvidia calls cores (stream processor).
The Tesla K40 has a total of 1920 process elements (15 CU * 128 PE in CU).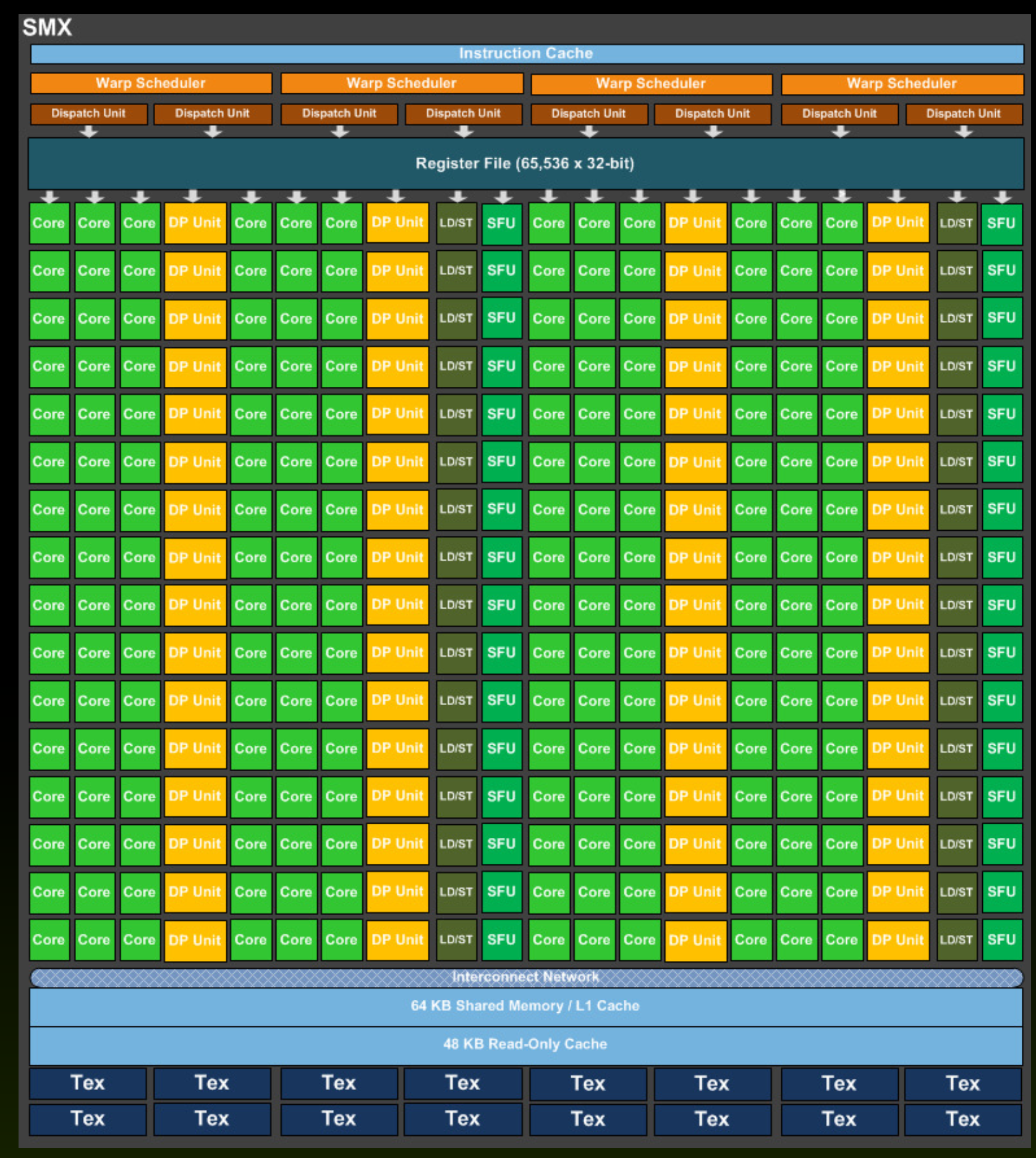
Implementing kernel
Kernel running on the GPU must be written in such a way that it is explicitly specified what each thread is doing. How we do this will be learned below. When a kernel is run on the GPU, the thread sorter, labeled as Giga Thread Engine, will first arrange the individual threads into compute units (CU). Within the compute units, the internal sorter will arrange the individual threads by process elements. The number of threads that GPU executes and sorts simultaneously is limited. There is also a limited number of threads that can be sorted and executed by individual compute units. A more detailed description of implementation and limitations in sorting and implementing threads will be given in the next section. -
Execution model
Graphical process units with a large number of process elements are ideal for accelerating problems that are data parallel. These are problems in which the same operation is performed on a large number of different data. Typical data parallel problems are computing with large vectors / matrices or images, where the same operation is performed on thousands or even millions of data simultaneously. If we want to take advantage of such massive parallelism offered to us by GPUs, we need to divide our programs into thousands of threads. As a rule, a thread on a GPU performs a sequence of operations on a particular data (for example, one element of the matrix), and this sequence of operations is usually independent of the same operations that other threads perform on other data. The program written in this way can be transferred to the GPU, where the internal sorters will arrange for sorting threads by compute units (CU) and process elements (PE). The English term for thread in the terminology used in OpenCL is work-item.
Threads are sorted on GPU in two steps:
- The programmer must explicitly divide individual threads into work-groups within the program. Threads in the same working group will be implemented on the same compute unit. Because the compute units have built-in local memory that is accessible to all threads on it, they will be able to exchange data quickly and easily without using the slower global GDDR5 memory on the GPU. In addition, the threads on the same compute unit can be synchronized with each other quite easily. The main sorter on the GPU will classify the workgroups evenly across all compute units. The working groups are classified into compute units completely independently of each other and in any order. Several working groups can be sent to one compute unit for implementation (today typically a maximum of 16).
- The sorter in the calculation unit will send threads from the same workgroup to process elements for implementation. It sends exactly 32 threads to each cycle for execution. We call these threads a warp. The bundle always contains 32 consecutive threads from the same workgroup. All threads in the bundle start at the same place in the program, but each has its own registers, including the program counter. Such a chamois even in a bundle can be arbitrarily branched, although this is not desirable. The best efficiency in bundle execution is achieved when all threads execute the same sequence of commands over different data (lock-step execution). If threads in a bundle execute jump commands, branching differently, their execution is serialized until they all come to the same command again, greatly reducing execution efficiency. Therefore, as programmers, we must make sure that there are no unnecessary branches (if-else statements) inside the thread. The implementation of the threads in bundles is shown in the figure below.
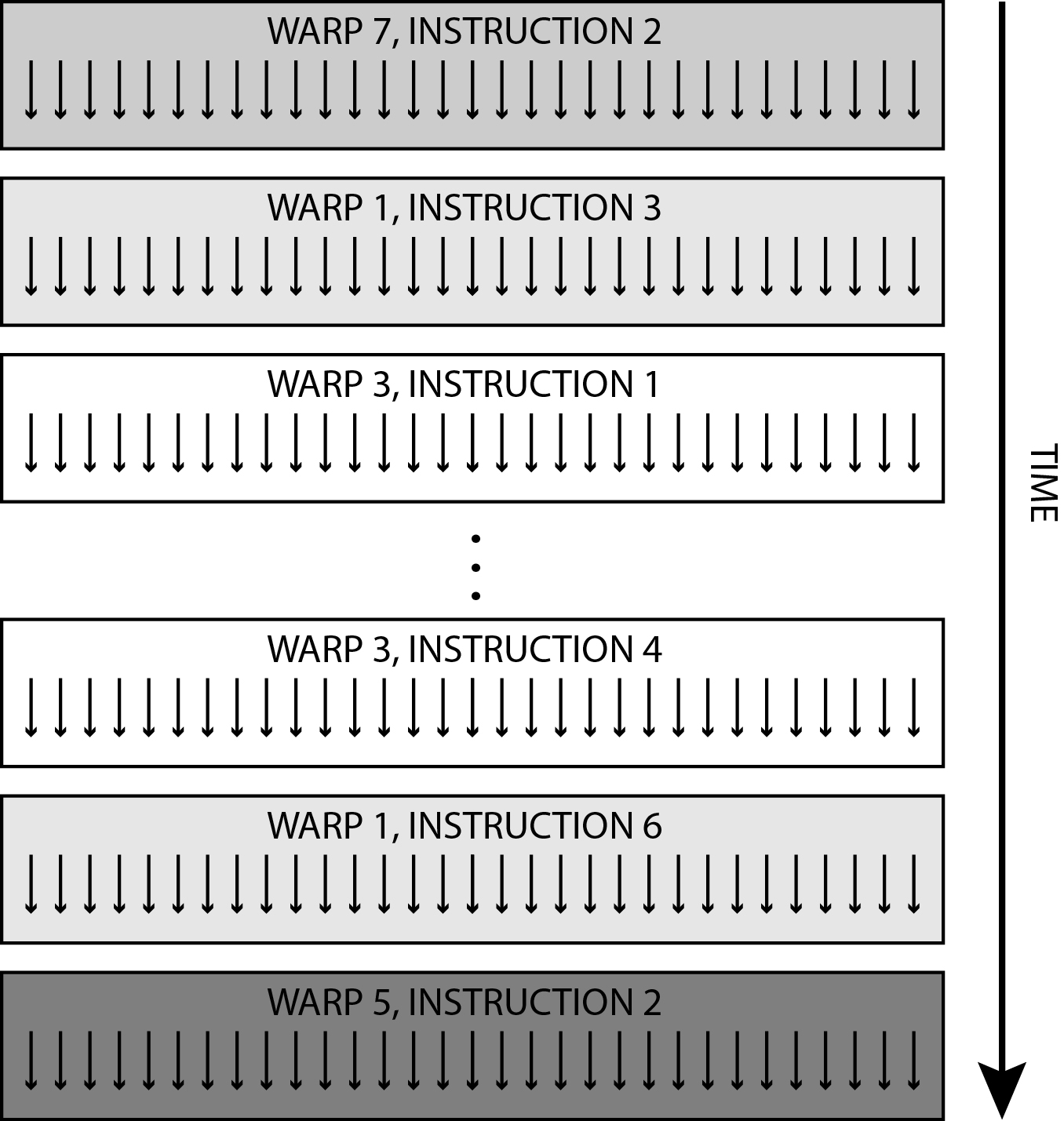The number of threads in one working group is limited upwards. There is also a limited number of working groups that are assigned to one compute unit at the same time and the number of threads that are allocated to one compute unit. For the Tesla K40, the maximum number of threads in a workgroup is 1024, the maximum number of workgroups on one calculation unit is 16 and the maximum number of threads that can be executed on one calculation unit is 2048. It follows from the latter that a maximum of 64 (2048/32) bundles.
We usually do smaller workgroups in programs that contain 128 or 256 threads. In this way, we can perform several working groups on the compute unit (for 256 threads in group 8, for 128 threads in working group 16 and for 1024 threads in working group 2) and thus facilitate the work of the sorter, which performs bundles from different working groups in any in order. This is especially true when threads from one workgroup are waiting before locking (synchronizing) and the sorter can send a bundle of threads from another workgroup into execution.
The image below shows the compute unit in the Tesla K40 GPU.
Each compute unit as four bundle sorters (marked as warp schedulers in the figure), so four bundles can be executed at the same time. In addition, each bundle sorter issues two commands at a time in execution (it has two dispatch units) from the same bundle of threads, which means that it can issue eight commands at a time - so that eight bundles are run at a time. In this way, they ensured that all process units were occupied at all times. We have not mentioned them so far, but in addition to 192 process elements, each calculation unit contains 64 units for floating-point calculation with double precision (DP unit) and 32 units for special operations, such as trigonometric operations (SFU - Special Functions). Unit). The figure below shows the operation of one beam sorter.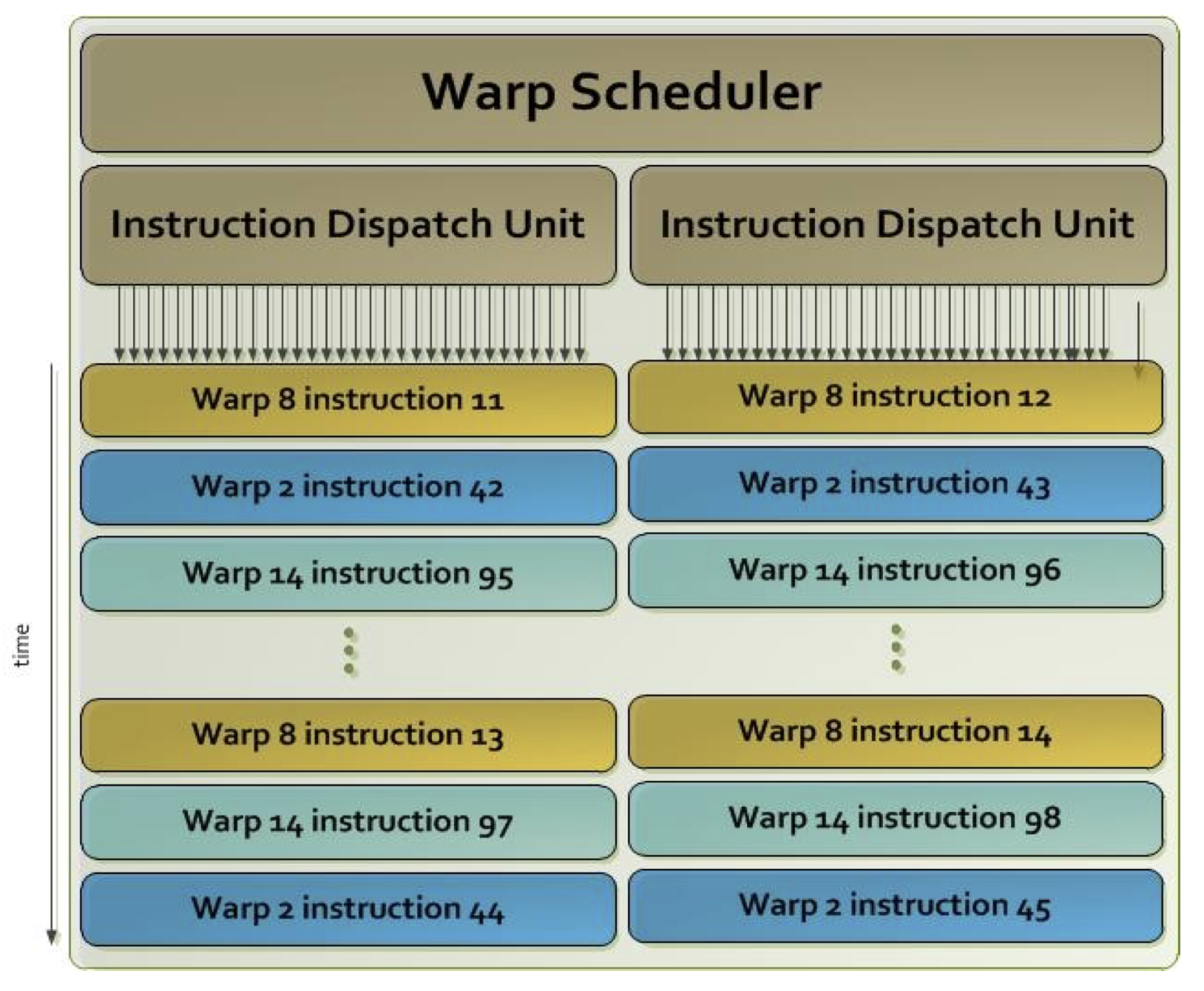
We see that two commands from the same beam are issued at any given time. The order of execution of the bundles is arbitrary and usually depends on the readiness of the operands.
The table below summarizes the maximum values of individual parameters in the Tesla K40.Limitations in Tesla K40 Number of threads in the bundle 32 Maximum number of beams in the calculation unit 64 Maximum number of threads in the calculation unit 2048 Maximum number of threads in group 1024 Maximum number of working groups in the calculation unit 16 Maximum number of registers per thread 255 The maximum size of local memory in the calculation unit 48 kB -
Memory hierarchy
GPUs contain various memories that are accessed by individual process elements or individual threads. The image below shows the memory hierarchy on the GPU.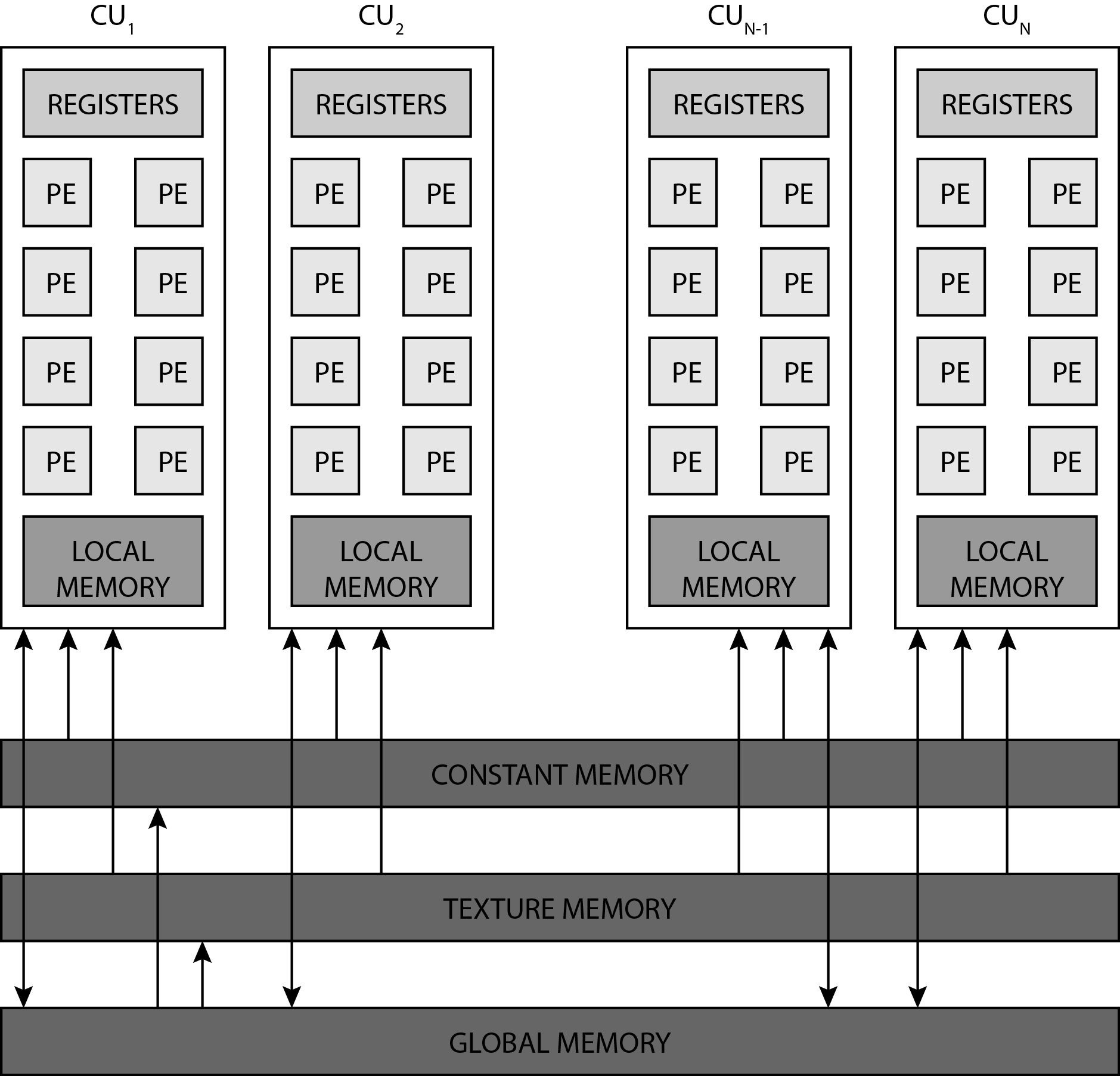
Registers
Each compute unit (CU) contains several thousand registers, which are evenly distributed among the individual threads. The registers are private for each thread. The compute unit in the Tesla K40 has 65,536 registers and each thread can use a maximum of 255 registers. Threads keep the most frequently accessed operands in the registers. Suppose we have 120 working groups with 128 threads each. On the Tesla K40 with 15 calculation units, we will have eight working groups per calculation unit (120/15 = 8), with each thread receiving up to 64 registers (65536 / (8 * 128) = 64).Local memory
Each compute unit has a small and fast SRAM (static RAM) memory, which is usually automatically divided into two parts during program startup:- first-level cache (L1) and
- local memory that can be used on either compute unit
With the Tesla K40 accelerator, this memory is 64kB in size and can be shared in three different ways:- 16 kB L1 and 48kB local memory,
- 32 kB L1 and 32 kB local memory
- 48 kB L1 and 16kB local memory.
As a rule, local memory is used for communication between threads within the same compute uint (threads exchange data with the help of local memory).Global memory
It is the largest memory porter on the GPU and is common to all threads and all compute units. The Tesla K40 is implemented in GDDR5. Like all dynamic memories, it has a very large access time (some 100 hour period). Access to main memory on the GPU is always performed in larger blocks or segments - with the Tesla K40 it is 128 bytes. Why segment access? Because the GPU forces the threads in the item bundle to simultaneously access data in global memory. Such access forces us into data parallel programming and has important implications. If threads in a bundle access adjacent 8-, 16-, 24-, or 32-bit data in global memory, then that data is delivered to the threads in a single memory transaction because they form a single segment. However, if only one thread from the bundle accesses a data in global memory (for example, due to branches), access is performed to the entire segment, but unnecessary data is discarded. However, if two threads from the same bundle access data belonging to two different segments, then two memory accesses are required. It is very important that when threading our programs, we ensure that memory access is grouped into segments (memory coalescing) - we try to ensure that all threads in the bundle access sequential data in memory.Constant and texture memories
Constant and texture memories are just separate areas in global memory where we store constant data, but they have additional properties that allow easier access to data in these two areas: - constant data in constant memory is always cached, this memory allows sending a single data to all threads in the bundle at once (broadcasting), - constant data (actually images) in the texture memory is always cached in the cache, which is optimized for 2D access; this speeds up access to textures and constant images in global memory.
-
-
-
OpenCL
So far, we have learned how the GPU is built, what the compute units and process elements are, how the programs run on it, how the workgroups and threads are arranged, and what the GPU memory hierarchy is. Now is the time to look at what the software model is.OpenCL framework
OpenCL (Open Computing Language) is an open source framework designed for parallel programming of a wide range of heterogeneous systems. OpenCL contains the OpenCL C programming language, designed to write program code that will run on devices (such as GPU or FPGA). We have learned before that we call such programs kernels. The same kernel executes all threads on the GPU. Unfortunately, OpenCL has one major drawback: it is not easy to learn. Therefore, before we can write our first program in OpenCL, we need to learn some important concepts.Platform and devices
OpenCL sees a general heterogeneous system as a platform consisting of a host and one or more different devices. Devices are usually GPU or FPGA accelerators. The platform is shown in the image below.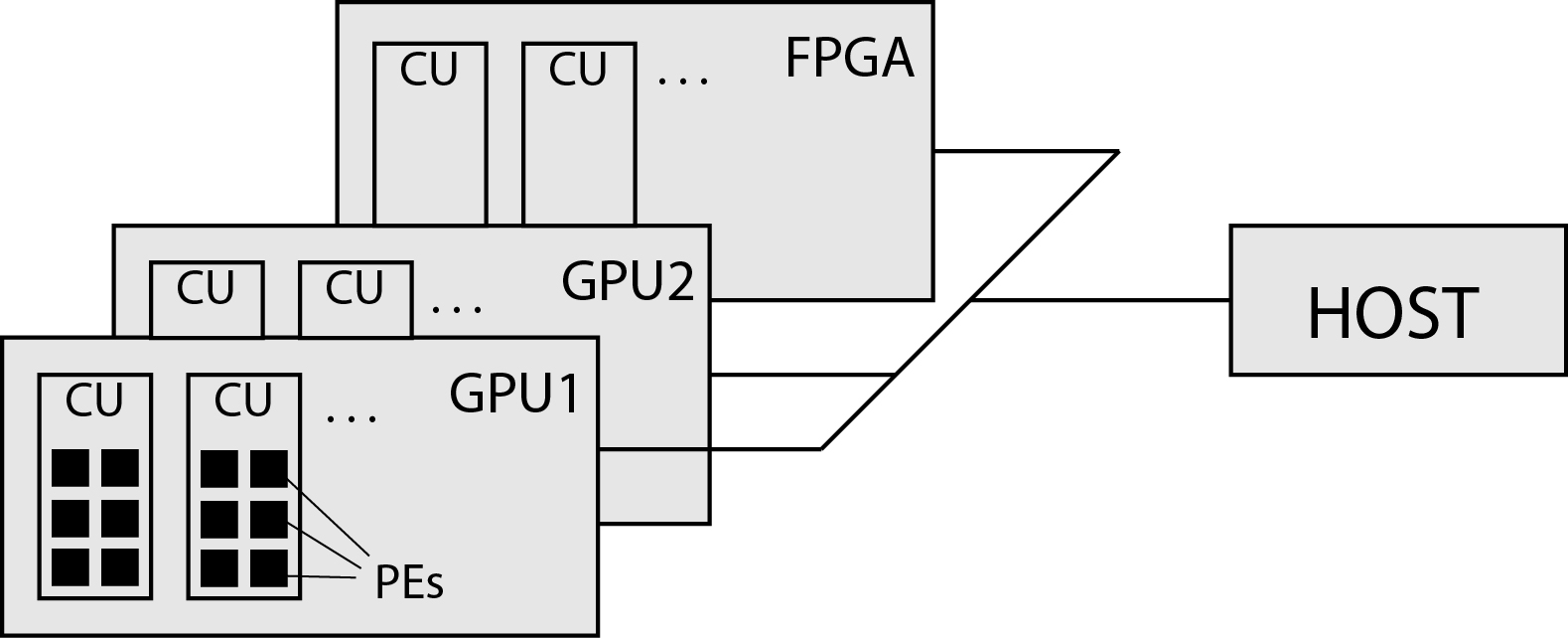
Each program in OpenCL consists of two main parts:
- code running on the host program, and
- one or more kernels running on the device.
OpenCL implementation model
We have already met the GPU implementation model before. We learned about compute units (CU) and process elements (PE) and threads and groups of threads. OpenCL uses a similar abstraction - a kernel executes a large number of threads simultaneously. These are grouped into working groups. Threads in workgroups can share data over local memory and can be synchronized with each other.
Each thread has its own unique identifier (ID). In principle, IDs are neither one-, two-, or three-dimensional, and are given with integers. For the purposes of the most comprehensible explanation, we will limit ourselves to two dimensions below. Thread indexing is always adapted to the spatial organization of the data. For example, if our data is vectors, we will neither index in one dimension, but if our data is a matrix or image, we will not index in two dimensions. Thus, OpenCL allows us to spatially organize threads in the same way as data. For example, in the case of images, the indexes of the threads will coincide with the indexes (coordinates) of the image points. In OpenCL terminology, we call thread space NDRange. We also index working groups in one-, two- or three-dimensional space. An example of two-dimensional indexing is shown in the figure below.
Each thread in the 2D space of the NDRange has two pairs of indexes:- global index (global ID) and
- local index (local ID).
OpenCL memory model
OpenCL contains an abstraction of the memory hierarchy on the GPU shown in the figure below.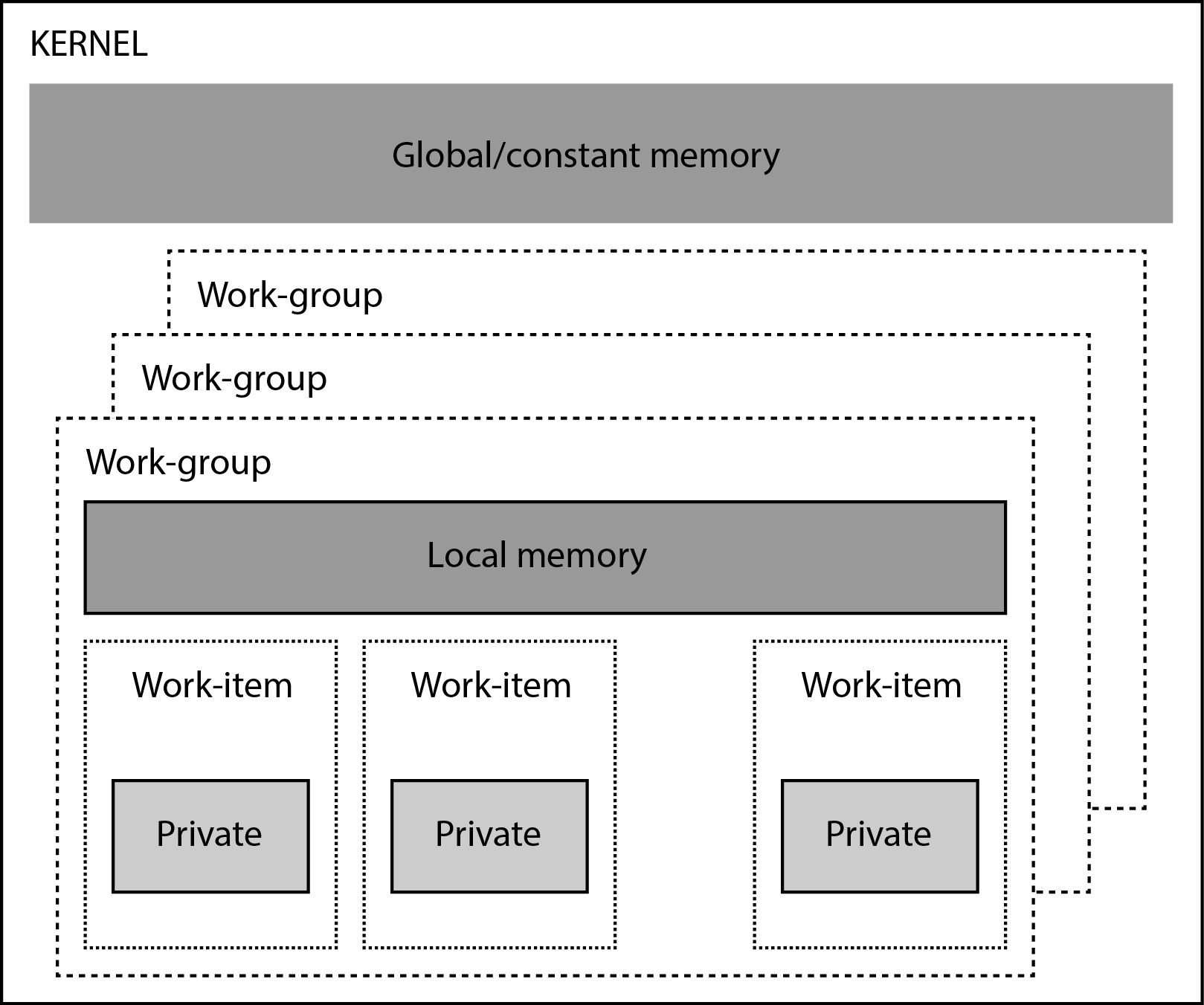
The memories provided by OpenCL are:
- We store variables in private memory that will be private for each thread. In GPU, private memory is represented by registers of arithmetic elements. If we want a variable to be private to a thread, then we need to declare it with the __private complement. In OpenCL, all variables are private by default and no add-on needs to be specified.
- We store variables in local memory that we want to be visible to all threads in the same workgroup. If we want a variable to be stored in local memory, we add the __local extension to the declaration.
- In global memory, we store variables that we want to be visible to all threads from all workgroups in the NDRange thread space. If we want a variable to be stored in global memory, we must declare it with the __global extension.
- Constant memory is the part of global memory that does not change during execution. If we want a constant to be stored in global memory, we use the __constant suffix next to the declaration.
-
-
-
Addition of vectors
Let’s start with a simple example of adding two vectors. We will solve the problem in two ways. First, we’ll start out quite naively and focus only on the basics of GPU programming and the steps on the host that are needed to run our first program on GPU. In the second mode, we will then focus on the kernel improvement implemented on the GPU.
The code below shows the implementation of a function in C for summing two vectors whose elements are real numbers, represented by floating-point notation with single precision (float).1 2 3 4 5 6 7 8 9 10 11 12 13
// add the elements of two arrays void VectorAdd(float *vecA, float *vecB, float *vecC, int iNumElements) { int iGID = 0; while (iGID < iNumElements) { vecC[iGID] = vecA[iGID] + vecB[iGID]; iGID += 1; } }The arguments of the function are the addresses of all three vectors (vecA, vecB, vecC) and the number of elements in the vectors (iNumElements). The vectors are summed by summing all the identical elements in the input vectors vecA and vecB and saving the result in the equilateral element of the vector vecC. Since the vectors have iNumElements elements, we will add the vectors in a loop that will repeat the iNumElements times.
In the loop, individual elements of the vector are indexed with the integer index iGID. We chose the name on purpose (Global Index), the reason for such a choice will be known to us soon.A naive attempt to add vectors
We would now like to run the VectorAdd() function on the GPU. We realized that GPUs are ideal for performing tasks where we have a lot of data parallelism - in our case this is even more true, since we perform the same operation (addition) over all elements of vectors. In addition, these operations are independent of each other (the elements of the vectors can be summed in any order) and can thus be summed in parallel.Kernel
In previous chapters, we learned that programs for GPU (kernels) are written in such a way that they can be executed (simultaneously) by all threads from the NDRange space (this will of course be defined below) - these are all threads that will be run on GPU . Therefore, we need to divide the work done by the VectorAdd() function as evenly as possible between the threads. In our case, this is a fairly simple task, as we will divide the work to begin with so that each thread will add only the same elements. Therefore, we will run as many threads on the GPU as there are elements in the vectors - in our case, this is the iNumElements thread.
All the iNumElements threads that we will run are made up of NDRange space. We have already mentioned that this space can be one-, two-, or three-dimensional and that we adjust the dimension of the space to the data. Since our vectors are one-dimensional fields, we will organize the NDRange space in our case in one dimension (X). The global size of this space will be iNumElements. Therefore, the global index of each thread that will run on the GPU will be uniquely determined from that space and will actually correspond to the index of the elements that the thread adds up. The kernel that all threads will run on the GPU is shown in the code below:1 2 3 4 5 6 7 8 9 10 11 12
__kernel void vecadd_naive ( __global float* vecA, __global float* vecB, __global float* vecC, int iNumElemements){ int iGID = get_global_id(0); if (iGID < iNumElemements) { vecC[iGID] = vecA[iGID] + vecB[iGID]; } }We see that the kernel code is very similar to the VectorAdd() function code. Each function we want to perform on the GPU must be declared as a kernel (__kernel). We named the kernel vecadd_naive (), and its arguments are the titles of the vectors and the number of elements in the vectors. The vector addresses this time have the __global specifier, which determines that these addresses refer to the global memory on the GPU. The vectors we want to add to the GPU must be stored on the GPU, because the compute units on the GPU cannot address the main memory on the host. Because vectors can be quite large, global memory is the only suitable memory space for storing vectors. In addition, all compute units can address global memory and therefore the vector elements will be accessible to all threads, regardless of which compute unit each thread will run on (we have no influence on this anyway).
Each thread first determines its global iGID index in the NDRange space with the get_global_id(0) function. Argument 0 when calling a function specifies that we require an index in dimension X. Then each thread sums identical elements in vectors whose index is equal to its index, but only if its index is less than or equal to the number of elements in vectors (so in a kernel if sentence). In this way we provide two:
- the data with which each thread works are uniquely determined for each thread and there is no possibility that two threads might try to write to the same element of the vector vecC,
- memory access is grouped into segments where all threads in the same bundle access sequential 8-, 16-, 24-, or 32-bit data in memory (memory coalescing).
A detailed description of the OpenCL C programming language can be found on The OpenCL C Specification website.Host program
Once we have written the kernel, we need to translate it first. We translate the pins for the selected device, so we must first select the platform, the device within the platform, create the context and command line for each device as we learned in the previous chapter. With this, the work of the program on the host is far from over. The latter must now perform the following tasks:
- reserve space in main memory and initialize data on the host,
- reserve space in the device's global memory where we will store our vectors,
- read the device application from file to memory,
- compile a device program - the device program will be translated during the execution of the program on the host,
- create a kernel from the translated program, which we will run on the selected device,
- transfer data from the host to the device
- set kernel arguments,
- set the size and organization of the NDRange thread space,
- run the kernel on the device and
- read data from the global memory on the device after the kernel execution is complete.
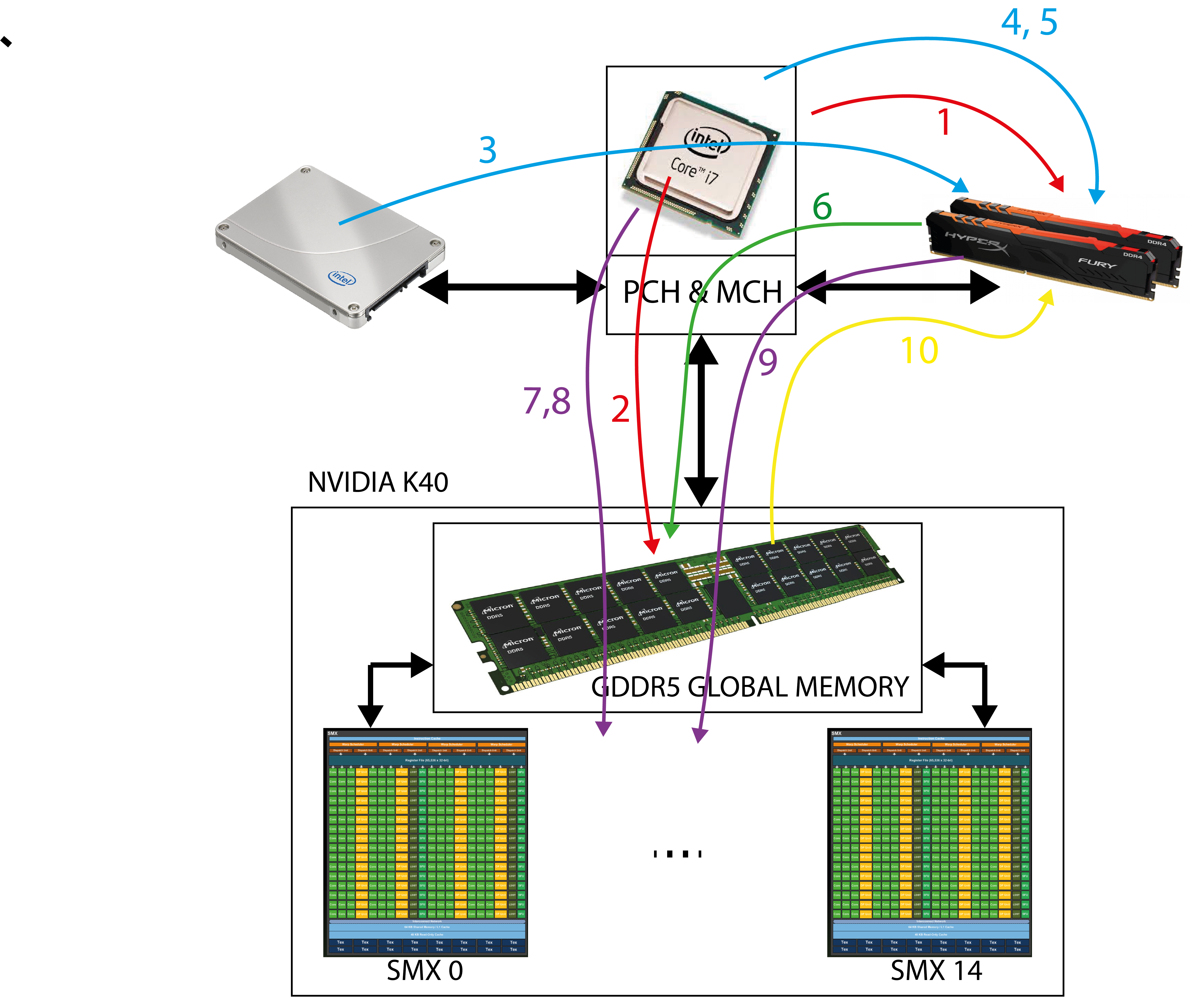The image above shows all the steps that a program must perform on the host before and after running the pins on the GPE device.Initialize data on the host
The program on the host must initialize all the data needed to compute on the device. We need to be aware that the host can only access its main memory and for now, all the data initialized by the host will be in the main memory. In our case, we need to reserve space for all three vectors and initialize the vectors we want to add:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
cl_float* vecA_h; cl_float* vecB_h; cl_float* vecC_h; int iNumElements = 256*4; // works for vectors with up to 1024 elements // Allocate host arrays vecA_h = (void *)malloc(sizeof(cl_float) * iNumElements); vecB_h = (void *)malloc(sizeof(cl_float) * iNumElements); vecC_h = (void *)malloc(sizeof(cl_float) * iNumElements); // init arrays: for (int i = 0; i<iNumElements; i++ ) { vecA_h[i] = 1.0; vecB_h[i] = 1.0; }We added _h to the names of the vectors we store on the host to emphasize that this is the data on the host. All elements of the input vectors on the host were set to 1.Reserve space in the device's global memory
We now need to reserve space in the device’s global memory where we will store all the vectors that occur in the computation. We use the clCreateBuffer() function to reserve space in the device's global memory. This reserves a datasize size space. When reserving space in the global memory, specify whether the device will only read from the reserved space (CL_MEM_READ_ONLY), only write to it (CL_MEM_WRITE_ONLY) or will have read and write access (CL_MEM_READ_WRITE). The clCreateBuffer() function returns a handler (type cl_mem) to a memory object (reserved space) in the device's global memory.Remember that the host (CPU) does not have direct access to this memory so never try to use this handler as a pointer and dereference it to the host!1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39
//*************************************************** // Create device buffers //*************************************************** cl_mem vecA_d; // Input array on the device cl_mem vecB_d; // Input array on the device cl_mem vecC_d; // Output array on the device // Size of data: size_t datasize = sizeof(cl_float) * iNumElements; // Use clCreateBuffer() to create a buffer object (d_A) // that will contain the data from the host array A vecA_d = clCreateBuffer( context, CL_MEM_READ_ONLY, datasize, NULL, &status); clerr_chk(status); // Use clCreateBuffer() to create a buffer object (d_B) // that will contain the data from the host array B vecB_d = clCreateBuffer( context, CL_MEM_READ_ONLY, datasize, NULL, &status); clerr_chk(status); // Use clCreateBuffer() to create a buffer object (d_C) // with enough space to hold the output data vecC_d = clCreateBuffer( context, CL_MEM_WRITE_ONLY, datasize, NULL, &status); clerr_chk(status);Reading kernelKernels are written in files with the .cl extension. In our case, the kernel.cl file will only contain a kernel of vecadd_naive(). In general, the kernel.cl file could contain any number of pliers and the functions that these pins call. We need to compile the program for the selected device, so we do this when the host already has all the information about the platform and devices. Before compiling, we need to read the program from the kernel.cl file into the host memory and then create a program object suitable for translation from it. We do this with the code below.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
//*************************************************** // Create a program object for the context //*************************************************** FILE* programHandle; // File that contains kernel functions size_t programSize; char *programBuffer; cl_program cpProgram; // 6 a: Read the OpenCL kernel from the source file and // get the size of the kernel source programHandle = fopen("kernel.cl", "r"); fseek(programHandle, 0, SEEK_END); programSize = ftell(programHandle); rewind(programHandle); printf("Program size = %lu B \n", programSize); // 6 b: read the kernel source into the buffer programBuffer // add null-termination-required by clCreateProgramWithSource programBuffer = (char*) malloc(programSize + 1); programBuffer[programSize] = '\0'; // add null-termination fread(programBuffer, sizeof(char), programSize, programHandle); fclose(programHandle); // 6 c: Create the program from the source // cpProgram = clCreateProgramWithSource( context, 1, (const char **)&programBuffer, &programSize, &status); clerr_chk(status); free(programBuffer);First we open the kernel.cl file and read the code from it and save it as a sequence of characters in the program string Buffer. Only then, with the clCreateProgramWithSource() function, do we read the programBuffer character string and create the appropriate translation object cpProgram from it.Compile the program for the selected GPE device
The translation of the read program, which is stored in the cpProgram object, is translated with the clBuildProgram() function, as shown in the code below.1 2 3 4 5 6 7 8 9 10 11 12
//*************************************************** // Build the program //*************************************************** status = clBuildProgram( cpProgram, 0, NULL, NULL, NULL, NULL); clerr_chk(status);We must be aware that only now, ie during the execution of the program on the host, the kernel, which we read from the kernel.cl file, is translated. Any errors in the code in kernel.cl will only appear now, during translation, and not when compiling the host program. Therefore, in the event of translation errors (for the clBuildProgram() function), they must be stored in a data set in main memory and displayed if necessary. This can be done with the clGetProgramBuildInfo() function:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
if (status != CL_SUCCESS) { size_t len; printf("Error: Failed to build program executable!\n"); // Firstly, get the length of the error message: status = clGetProgramBuildInfo(cpProgram, devices[0], CL_PROGRAM_BUILD_LOG, 0, NULL, &len); clerr_chk(status); // allocate enough memory to store the error message: char* err_buffer = (char*) malloc(len * sizeof(char)); // Secondly, copy the error message into buffer status = clGetProgramBuildInfo(cpProgram, devices[0], CL_PROGRAM_BUILD_LOG, len * sizeof(char), err_buffer, NULL); clerr_chk(status); printf("%s\n", err_buffer); free(err_buffer); exit(1); }The clGetProgramBuildInfo() function is called twice. First, to determine the length of the error message, and second, to read the entire error message. The following is an example of an error printout in the case where we used an undeclared name for vector B in a kernel:
Error: Failed to build program executable! <kernel>:9:35: error: use of undeclared identifier 'vecBB'; did you mean 'vecB'? vecC[myID] = vecA[myID] + vecBB[myID]; ^~~~~ vecB <kernel>:2:33: note: 'vecB' declared here __global float* vecB, ^Creating a kernel from a translated program
In general, our translated program could contain more kernels. So now we only create a kernel of vecadd_naive() from the program that we want to run on the device. We do this with the clCreateKernel() function.1 2 3 4 5 6 7 8 9 10 11
//*************************************************** // Create and compile the kernel //*************************************************** cl_kernel ckKernel; // Create the kernel ckKernel = clCreateKernel( cpProgram, "vecadd_naive", &status); clerr_chk(status);Data transfer to the device
The vectors that we initialized in the first step are transferred from the host's main memory to previously created memory objects in the device's global memory. Data transfer is actually triggered by writing the appropriate command to the cmdQueue device command line. We do this with the clEnqueueWriteBuffer() function.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
//*************************************************** // Write host data to device buffers //*************************************************** // Use clEnqueueWriteBuffer() to write input array A to // the device buffer bufferA status = clEnqueueWriteBuffer( cmdQueue, vecA_d, CL_FALSE, 0, datasize, vecA_h, 0, NULL, NULL); clerr_chk(status); // Use clEnqueueWriteBuffer() to write input array B to // the device buffer bufferB status = clEnqueueWriteBuffer( cmdQueue, vecB_d, CL_FALSE, 0, datasize, vecB_h, 0, NULL, NULL); clerr_chk(status);Setting kernel arguments
In order to run the selected kernel vecadd_naive(), we need to set arguments to it. To do this, use the clSetKernelArg() function.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
//*************************************************** // Set the kernel arguments //*************************************************** // Set the Argument values status = clSetKernelArg(ckKernel, 0, sizeof(cl_mem), (void*)&vecA_d); status |= clSetKernelArg(ckKernel, 1, sizeof(cl_mem), (void*)&vecB_d); status |= clSetKernelArg(ckKernel, 2, sizeof(cl_mem), (void*)&vecC_d); status |= clSetKernelArg(ckKernel, 3, sizeof(cl_int), (void*)&iNumElements); clerr_chk(status);The second argument of the clSetKernelArg() function indicates the order of the argument when the clip is called.Setting up and organizing the NDRange space
We are just about to run the threads that will execute the selected kernel on the GPU device. We still need to determine how many threads we will run on the GPU device, how these threads will be organized into workgroups, and how the threads and workgroups will be organized in the NDRange space. We call this the NDRange space setting. For now, we will be working in the one-dimensional NDRange space, so its size and organization are determined by the following variables szLocalWorkSize and szGlobalWorkSize:
In the code above, we specified that we want to have 128 threads in the workgroup and that we want to run as many threads as the long vectors (iNumElements).1 2 3
// set and log Global and Local work size dimensions const size_t szLocalWorkSize = 128; const size_t szGlobalWorkSize = iNumElements;
Launch the kernel on the selected GPU deviceTo start the kernel on the selected device, write the command to run the kernel and the description of the NDRange space in the cmdQueue command line. We do both with the clEnqueueNDRangeKernel() function.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
//*************************************************** // Enqueue the kernel for execution //*************************************************** // Launch kernel status = clEnqueueNDRangeKernel( cmdQueue, ckKernel, 1, NULL, &szGlobalWorkSize, &szLocalWorkSize, 0, NULL, NULL); clerr_chk(status);In the code above, we said that we want to run a kernel of ckKernel, that the NDRange space has dimension 1, that its global size is szGlobalWorkSize, and that the threads are organized into szLocalWorkSize size workgroups.At this point, it should be noted that when we stop a command in the command line (for example, to transfer data or run a kernel), we have no influence on when the command will actually be executed. The clEnqueueWriteBuffer() and clEnqueueNDRangeKernel() functions are non-blocking and terminate immediately. So we don’t really know when the data will be transferred, when the kernel starts and ends running on the device. The type only provides us with the order of execution of commands in it. Thus, we can argue that the kernel will certainly not start running until the data is transferred from the host to the device.Reading data from GPU device
When the kernel is complete, the vector with the sums is transferred from the device's global memory to the host's main memory.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
//*************************************************** // Read the output buffer back to the host //*************************************************** // Synchronous/blocking read of results status = clEnqueueReadBuffer( cmdQueue, vecC_d, CL_TRUE, 0, datasize, vecC_h, 0, NULL, NULL); clerr_chk(status); // Block until all previously queued OpenCL commands in a command-queue // are issued to the associated device and have completed clFinish(cmdQueue);But how do we now know when the data will actually be copied and when we can access it? To do this, call the clFinish() function, which blocks the execution of the main program until the cmdQueue command type is emptied.
Erasing memory on the host
At the end of the program, we still need to free up all the reserved memory space on the host.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
//************************************************* // Cleanup //************************************************* if (srcA_h) free(vecA_h); if (srcB_h) free(vecA_h); if (srcC_h) free(vecA_h); if (platforms) free(platforms); if (devices) free(devices); if(ckKernel) clReleaseKernel(ckKernel); if(cpProgram) clReleaseProgram(cpProgram); if(cmdQueue) clReleaseCommandQueue(cmdQueue); if(context) clReleaseContext(context); if(srcA_d) clReleaseMemObject(srcA_d); if(srcB_d) clReleaseMemObject(srcB_d); if(srcC_d) clReleaseMemObject(srcC_d);The full code from this chapter can be found in the 02-vector-add-short folder here.
Addition of arbitrarily long vectors
The vecadd_naive() kernel we used to add the vectors has one drawback - each thread that the vecadd_naive() kernel performs will calculate only one sum. Recall that the number of threads that make up a workgroup is limited and that the number of threads that run simultaneously on one unit of account is also limited. With the Tesla K40 device, the maximum number of threads that are executed on one calculation unit at a time is 2048. Since the Tesla K40 device has only 15 calculation units, the maximum number of threads that can be executed at one time is 30,720. If we run more than that many threads, the driver will have to serialize their execution on the GPU. Therefore, it is much better to determine the maximum number of threads that we run from how many threads we will put in one workgroup, how many groups can be executed on one unit of account at a time, and how many units of account are on the GPU. In this case, we will probably have a smaller number of threads than the length of the vectors. We solve the problem with the bottom kernel.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
__kernel void VectorAdd_arbitrary(__global float* vecA, __global float* vecB, __global float* vecC, int iNumElements) { // get index into global data array int iGID = get_global_id(0); int iGS = get_global_size(0); while (iGID < iNumElements) { //add the vector elements vecC[iGID] = vecA[iGID] + vecB[iGID]; iGID = iGID + iGS; } }Now, each thread will first determine its global iGID index and the global size of the NDRange iGS space (this is actually the number of all active threads). It will then add the identical elements in the while loop by adding two identical elements in one iteration and then increasing the iGID by as many as all the active threads. Thus, it will move to the next two identical elements and add them up. The loop ends when the iGID index exceeds the size of the vectors.
Surely you are wondering why one thread would not add up an adjacent pair of identical elements or 4 adjacent pairs of identical elements? The reason lies in the memory access mode! Recall that memory is accessed in segments. To ensure coordinated memory access, two adjacent threads in the bundle must access two adjacent memory words.
The program on the host stays the same this time - only the second kernel needs to be loaded. You can also try to play with different vector sizes and different NDRange space settings yourself.
The full code from this chapter can be found in the 04-vector-add-arb folder here. -
Scalar product of vectors
Let’s try to play around with a little more interesting problem now. This time, instead of adding the vectors, we will program the scalar product of two vectors - we first multiply the identical elements with each other, and then we add the products.A naive approach
The first implementation of a scalar product will be similar to the summation of vectors. The idea is that threads on the GPU work products between identical elements of vectors, while the host sums all partial products. The kernel for the products of identical elements of vectors is:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
__kernel void DotProd_naive(__global float* vecA, __global float* vecB, __global float* vecC, int iNumElements) { // get index into global data array int iGID = get_global_id(0); int iGS = get_global_size(0); while (iGID < iNumElements) { //add the vector elements vecC[iGID] = vecA[iGID] * vecB[iGID]; iGID = iGID + iGS; } }After completing the kernel, the host must read the product vector from the device and add all its elements in a loop:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
/ Synchronous/blocking read of results status = clEnqueueReadBuffer( cmdQueue, vecC_d, CL_TRUE, 0, datasize, vecC_h, 0, NULL, NULL); clerr_chk(status); // Block until all previously queued OpenCL commands in a command-queue // are issued to the associated device and have completed clFinish(cmdQueue); // sum of partial products: float result = 0.0; for (int i=0; i<iNumElements; i++) { result += vecC_h[i]; }The full code from this chapter can be found in the 05-dot-product-naive folder here.
Scalar product with reduction and use of local memory
In the above example, the host must add up all the partial products. If the vectors are very long, the host will need a lot of time to transfer the partial products from the device, and then also add the partial products for quite some time. Therefore, we will now present a solution that will add up all the partial products. In doing so, we will learn how threads can use local memory and how they participate in computation. The calculation of the scalar product will consist of three steps:
- N threads will be divided into G working groups. Each thread in the working group will compute the partial products between the identical elements of the vectors and add them to its partial product, which it will store in the local memory. Since we will have L=N/G threads in the workgroup, we will have L partial products stored in the local memory at the end of this step.
- Then, all threads within one working group will work together to add up the L partial products in the working group and store their result in the intended place in the global memory of the device. For G workgroups, we will have at the end of this step G totals of partial products in the global memory of the device.
- We will now transfer only G totals from the device's global memory to the host and add them there. Because the workgroups G are much smaller than the size of the vectors N, the host will transfer significantly less data and have much less work to
add up.
Step 1: partial products in the group
The code below shows the part of the kernel responsible for multiplying the identical elements of the vectors and summing the products.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
int myGID = get_global_id(0); int myLID = get_local_id(0); int myWGID = get_group_id (0); __local float vecC_wg[64]; vecC_wg[myLID] = 0.0; while (myGID < iNumElemements) { vecC_wg[myLID] += vecA[myGID] * vecB[myGID]; myGID += get_global_size (0); } //-- wait at the barrier! barrier(CLK_LOCAL_MEM_FENCE);In our case, we will have 64 threads in one working group. First, in line 5, we declare the field in which each thread in the working group will store the sum of its products:
5
__local float vecC_wg[64];The __local extension specifies that the vecC_wg field is stored in local memory. Although this declaration is specified for each thread in the group, the compiler will create only one field in the local memory of the calculation unit, which will be common to all threads in the workgroup.
Then, in line 7, each thread initializes its element, which will store its sum of partial products.
The myLID value determines the index of the threads in the workgroup. Thus, each thread will initialize only the element of the field that belongs to it.
Now in the while loop (lines 9 to 12)9 10 11 12
while (myGID < iNumElemements) { vecC_wg[myLID] += vecA[myGID] * vecB[myGID]; myGID += get_global_size (0); }each thread multiplies the identical elements of the vectors corresponding to its global index and counts the products in vecC_wg [myLID].
Before we add all the elements of the vecC_wg [myLID] field in the second step, we need to make sure that all the threads in the group have completed the execution of the while loop. We say that the threads have to wait at the barrier. Obstacles in OpenCL are implemented with the barrier function (CLK_LOCAL_MEM_FENCE). The function blocks the further execution of the program until it is called by everyone in the working group. In other words, all threads in the workgroup must call the barrier function (CLK_LOCAL_MEM_FENCE) before any thread can continue running the program.Step 2: sum of partial products in the group
In the second step, we need to add all the elements of the vecC_wg [myLID] field. We would naively solve this by adding only one thread in the working group to all these elements. However, there is a better solution shown in the image below: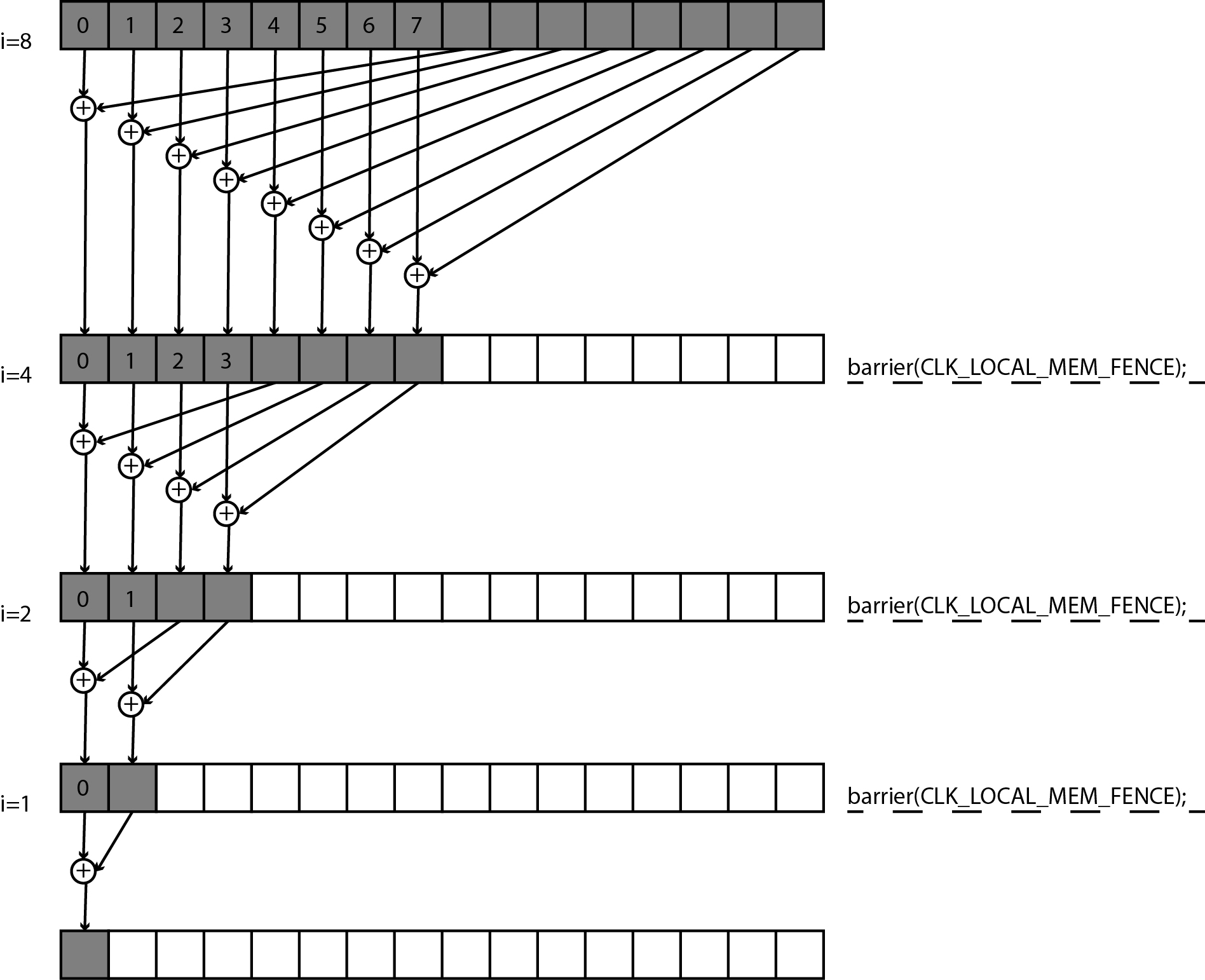
We will use a procedure called reduction to add the elements. Suppose we have only 16 elements to add up and 16 threads in a working group. In the first step, each of the first eight threads in the workgroup will add an element with its myLID index and an element with its myLID + 8 index and write the sum in an element with its myLID index. The remaining eight threads in the working group will not do anything. Then all the threads will wait at the obstacle. In the next step, only each of the first four threads will add an element with its myLID index and an element with its myLID + 4 index, the other threads will not add up. Before continuing with the work, all the threads will again wait in front of the obstacle. Thus, we will continue the process until there is only one thread with index 0 left, which will add up the element with index 0 and the element with index 1. The reduction procedure just described is shown by the code below in lines 24 to 34.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
__kernel void DotProd_reduction (__global float* vecA, __global float* vecB, __global float* localproducts, int iNumElemements) { int myGID = get_global_id(0); int myLID = get_local_id(0); int myWGID = get_group_id (0); __local float vecC_wg[64]; vecC_wg[myLID] = 0.0; while (myGID < iNumElemements) { vecC_wg[myLID] += vecA[myGID] * vecB[myGID]; myGID += get_global_size (0); } //-- wait at the barrier! barrier(CLK_LOCAL_MEM_FENCE); localproducts[myWGID] = 0.0; // Reduction: int i = get_local_size (0) / 2; while (i != 0) { if (myLID < i) { //perform the addition: vecC_wg[myLID] += vecC_wg[myLID + i]; } i = i/2; // wait at the barrier: barrier(CLK_LOCAL_MEM_FENCE); } // only one WI writes the result: if (myLID == 0) { localproducts[myWGID] = vecC_wg[0]; } }An attentive reader will notice that the barrier function (CLK_LOCAL_MEM_FENCE) is called by all threads in the group and not just those that add up. The reason is that the barrier function (CLK_LOCAL_MEM_FENCE) requires that all threads in the group execute it before any thread can continue working. If the barrier function (CLK_LOCAL_MEM_FENCE) were naively placed in a branch (if statement), the execution of the kernel would stop forever at the obstacle, as the threads that reach the obstacle would wait for all the remaining threads in the group that did not perform the branch.
At the end of the reduction, the sum of all elements in the vecC_wg [myLID] field will be written in the vecC_wg[0] element. Finally, a thread with myLID=0 will overwrite this result in the device's global memory in the localproducts field to a location with an index corresponding to the index of the myWGID workgroup (lines 36 to 39):36 37 38 39
// only one WI writes the result: if (myLID == 0) { localproducts[myWGID] = vecC_wg[0]; }The program on the host this time requires minor changes. The partial results that we will read from the device will now be contained in the vecC_d field, which will have only as many elements as there are workgroups:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
const size_t szLocalWorkSize = 64; const size_t szGlobalWorkSize = 2048; int iNumGroups = (int)(szGlobalWorkSize / szLocalWorkSize); size_t datasizeC = sizeof(cl_float) * iNumGroups; // Use clCreateBuffer() to create a buffer object (d_C) // with enough space to hold the output data vecC_d = clCreateBuffer( context, CL_MEM_WRITE_ONLY, datasizeC, NULL, &status); clerr_chk(status);In the code above, we assumed that we run only 2048 threads and that each workgroup has 64 threads.
Finally, the host must read the partial products of the individual working groups and add them up.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
// Synchronous/blocking read of results status = clEnqueueReadBuffer( cmdQueue, vecC_d, CL_TRUE, 0, datasizeC, vecC_h, 0, NULL, NULL); clerr_chk(status); // Block until all previously queued OpenCL commands in a // command-queue are issued to the associated device and have completed clFinish(cmdQueue); // check the result float result = 0.0; for (int i=0; i<iNumGroups; i++) { result += vecC_h[i]; }The full code from this chapter can be found in the 06-dot-product-reduction folder here.
Measuring kernel execution time
The execution time of kernel on the GPU can also be measured. For this we use the t.i. events - GPU devices can be required to report all events related to commands that we send by command line. Two interesting events are the beginning and the end of the kernel implementation. To measure the execution time of a kernel we need to:
- Enable the use of events when creating command types:
1 2 3 4 5
cmdQueue = clCreateCommandQueue( context, devices[0], CL_QUEUE_PROFILING_ENABLE, // enable profiling &status);- The command to start the kernel is associated with the event (last argument)
1 2 3 4 5 6 7 8 9 10 11 12 13
cl_event event; // Launch kernel status = clEnqueueNDRangeKernel( cmdQueue, ckKernel, 2, NULL, szGlobalWorkSize, szLocalWorkSize, 0, NULL, &event); // link to event clerr_chk(status);- after starting the kernel we are waiting for the event:
1
clWaitForEvents(1, &event);When we transfer the results from the GPU back to the host, we use the OpenCL API of the clGetEventProfilingInfo function to read the time of the two events CL_PROFILING_COMMAND_START and CL_PROFILING_COMMAND_END and calculate the difference between them:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
cl_ulong time_start; cl_ulong time_end; clGetEventProfilingInfo(event, CL_PROFILING_COMMAND_START, sizeof(time_start), &time_start, NULL); clGetEventProfilingInfo(event, CL_PROFILING_COMMAND_END, sizeof(time_end), &time_end, NULL); double nanoSeconds = time_end-time_start; printf("Kernel Execution time is: %0.3f milliseconds \n",nanoSeconds / 1000000.0);The full code from this chapter can be found in the 07-dot-product-profiling folder here.
-
Matrix multiplication
We are now tackling a problem that will help us understand the 2-dimensional space of the NDRange and the use of local memory to speed up kernel implementations on GPU devices. For this purpose, we will program the multiplication of matrices. Without loss of generality, we will confine ourselves to square matrices of size NxN. The multiplication of the square matrices A and B is shown in the figure below:
The element of the matrix C [i, j] is obtained by scalarly multiplying the i-th row of the matrix A and the j-th column of the matrix B. So, for each element of the matrix C we have to calculate one scalar product between the row from A and the column from B. the figure shows which rows and columns need to be scalarly multiplied by each other to obtain the elements C [1,2], C [5,2] and C [5,7]. For example, for C [5,7] we need to scalarly multiply the 5th row from matrix A and the 7th column from matrix B.
Naive matrix multiplication
With a simple version of matrix multiplication, we will first learn about the use of two-dimensional NDRange spaces.Kernel
This time, we’re not going to deal with the effectiveness of a kernel yet. We will prepare it so that each thread it will perform will calculate only one element of the product matrix.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
__kernel void matmul_naive( __global float* matA, __global float* matB, __global float* matC, int N){ int i = get_global_id(1); // row (Y) int j = get_global_id(0); // column (X) float dp; dp = 0.0; for (int k = 0; k < N; k++){ dp += matA[i*N + k] * matB[k*N + j]; } matC[i*N + j] = dp; }Since the elements of the matrices are organized in a 2-dimensional field, it is most natural that we also organize the threads into a two-dimensional space NDRange. Each thread will now be defined by a pair of global indexes (i, j). In the above code, therefore, each thread first obtains its global index by calling the get_global_id function (lines 8 and 9).
8 9
int i = get_global_id(1); // row (Y) int j = get_global_id(0); // column (X)Each thread then calculates the scalar product between the i-th row in matrix A and the j-th column in matrix B and stores the result in element C [i, j] of the product matrix (rows 13 to 18).Host program
The program on the host must reserve space for all three matrices on the host and initialize matrices A and B and reserve space in the device's global memory for three NxN size matrices (lines 20 to 34)20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
cl_float* matA_h; cl_float* matB_h; cl_float* matC_h; // Size of data: size_t datasize = sizeof(cl_float) * iNumElements * iNumElements; // Allocate host arrays matA_h = (void *)malloc(datasize); matB_h = (void *)malloc(datasize); matC_h = (void *)malloc(datasize); // init arrays: for (int i = 0; i<iNumElements; i++ ) { for (int j = 0; j<iNumElements; j++ ) { matA_h[i*iNumElements + j] = 1.0; matB_h[i*iNumElements + j] = 1.0; } } cl_mem matA_d; // Input array on the device cl_mem matB_d; // Input array on the device cl_mem matC_d; // Output array on the device s // Use clCreateBuffer() to create a buffer object (d_A) // that will contain the data from the host array A matA_d = clCreateBuffer( context, CL_MEM_READ_ONLY, datasize, NULL, &status); clerr_chk(status); // do the same for matB_d an d matC_d ...In addition, the program on the host must set the global size of the NDRange space and the number of threads in the workgroup.
1 2
const size_t szLocalWorkSize[2] = {16, 16}; const size_t szGlobalWorkSize[2] = {N, N};In the example above, we determined that we would run NxN threads in two-dimensional NDRange space, and that each workgroup would contain 16x16 threads.The kernel on the GPU device is started with the clEnqueueNDRangeKernel function, where the third argument determines that the NDRange space is two-dimensional.1 2 3 4 5 6 7 8 9 10
status = clEnqueueNDRangeKernel( cmdQueue, ckKernel, 2, NULL, szGlobalWorkSize, szLocalWorkSize, 0, NULL, NULL);Multiplication of matrices by tiles using local memory
The previous matrix multiplication code has quite a few serious flaws. Each thread reads 2xN elements from the global memory: a row from matrix A and a column from matrix B. On close observation we see that all threads that compute an element of matrix C in the same row access the same row of matrix A, but each to a different column of matrix B. Worst of all, when accessing columns in matrix B, we do not consider coordinated access to global memory. Adjacent threads do not access adjacent elements of matrix B, which greatly slows down the execution of the kernel, as two adjacent elements in a column can be more than 128 bytes apart in long rows and fall into different segments. In such a case, a separate memory access is required for each column element from matrix B!
On the other hand, it is known that the multiplication of matrices can be performed by tiles - we multiply smaller submatrices (tiles), as shown in the figure below.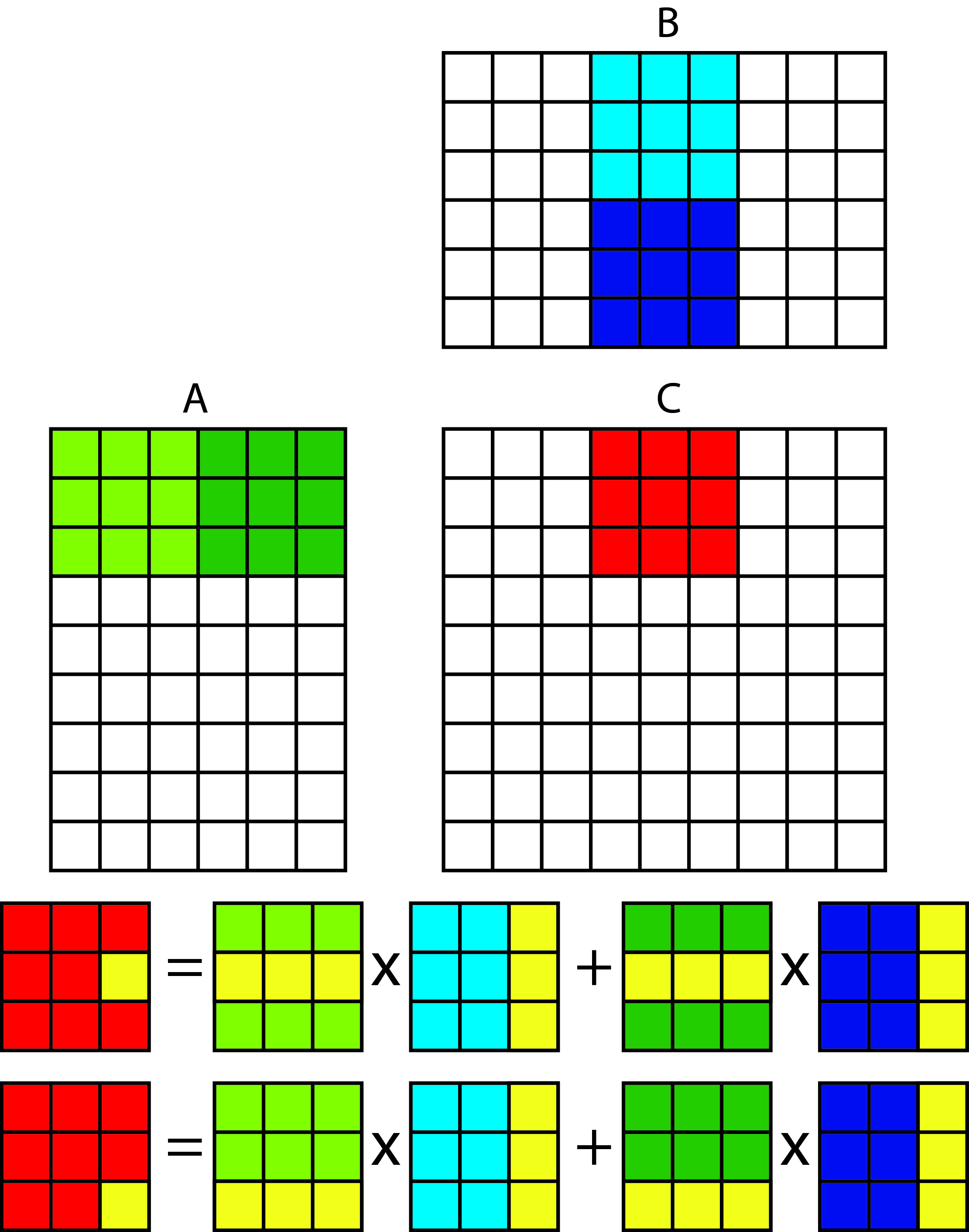
We will therefore obtain the same result if we calculate the elements of submatrix C gradually by multiplying the submatrices (tiles) of matrix A and matrix B. Following the picture above, the idea is as follows: First load the light green plate of matrix A and the light blue plate of matrix B into the local memory and make them together. Thus we get a partially calculated red tile of matrix C. In the next step we load a dark green tile from matrix A and a dark blue tile from matrix B, multiply them and add the result to the red tile from matrix C. Since in some step both tiles from matrices A and B in local memory, we have no problem with coordinated access to global memory. On top of that, access to local memory is 100 times faster than access to global memory!The kernel that multiplies the matrix by tiles is represented by the code below.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
#define TW 16 __kernel void matmul_tiled( __global float* matA, __global float* matB, __global float* matC, int N){ // Local memory to fit the tiles __local float tileA[TW][TW]; __local float tileB[TW][TW]; // global thread index int rowGID = get_global_id(1); // row in NDRange int colGID = get_global_id(0); // column in NDRange // local thread index int rowLID = get_local_id(1); // row in tile int colLID = get_local_id(0); // column in tile float dp = 0.0; // Iterate through all the tiles necessary to calculate the products: for (int iTile = 0; iTile < N/TW; iTile++){ // Collaborative load of tiles: // - Load a tile of matrix A into local memory: tileA[rowLID][colLID] = matA[rowGID*N + (colLID + iTile*TW)]; // - Load a tile of matrix B into local memory: tileB[rowLID][colLID] = matB[(rowLID + iTile*TW)*N+colGID]; // Synchronise to make sure the tiles are loaded barrier(CLK_LOCAL_MEM_FENCE); for(int k = 0; k < TW; k++) { dp += tileA[rowLID][k] * tileB[k][colLID]; } // Wait for all WI to finish before loading next tile: barrier(CLK_LOCAL_MEM_FENCE); } // save the dot product into matrix C in global memory: matC[rowGID*N + colGID] = dp; }Each thread in the for loop walks through all the tiles needed to calculate its element of the matrix C (lines 23 to 38).
23 24 25
for (int iTile = 0; iTile < N/TW; iTile++){ ... }In each iteration, the for loops of the threads from the same workgroup first transfer the tiles from matrix A and matrix B to the local memory and wait at the obstacle (lines 24 to 31).
24 25 26 27 28 29 30 31 32
// Collaborative load of tiles: // Load a tile of matrix A into local memory: tileA[rowLID][colLID] = matA[rowGID*N + (colLID + iTile*TW)]; // Load a tile of matrix B into local memory: tileB[rowLID][colLID] = matB[(rowLID + iTile*TW)*N+colGID]; // Synchronise to make sure the tiles are loaded barrier(CLK_LOCAL_MEM_FENCE); }Here we need to stop for a moment and explain the indexes we use when reading tiles from the device’s global memory. Assume that the tiles are of dimension TWxTW, where TW = 4, and that N = 8. Assume that the thread computes element C [5,2]. This element belongs to a tile with an index (1.0). The thread responsible for calculating element C [5,2] has a global index (5,2) and a local index (1,2). This thread must now access tiles (1,0) and (1,1) from matrix A and tiles (0,0) and (1,1) from matrix B. Thread (5,2) will be in charge of loading the following elements to local memory:- A (5,2) and B (1,2) in the first iteration and
- A (5.6) and B (5.2) in the second iteration.
The figure below shows the relationship between the local index of each tile element, and the local and global index of the thread it reads.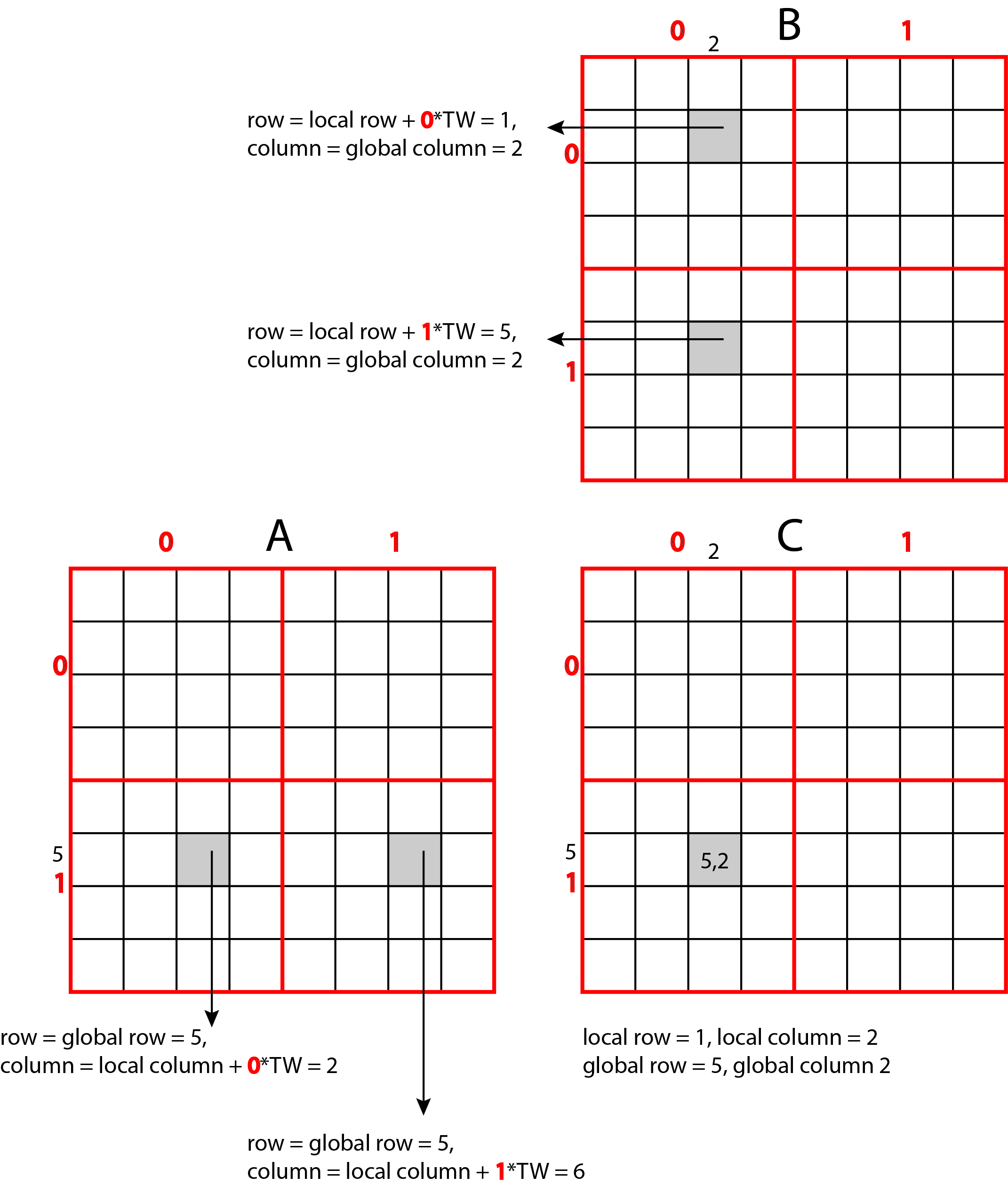
The code on the host will remain the same as in the naive multiplication of matrices, we just need to load a kernel of matmul_tiled.
The full code from this chapter can be found in the 08-matrix-mul folder here. -
Image processing
Edge enhancement is an image filter that increases the contrast of edges. The edge is defined as a significant local change in image intensity. At the ideal step, the intensity change occurs in a single pixel step. Ideal edges are very rare in images, especially if the images are smoothed beforehand to remove noise from them. Changes in intensity therefore occur at several consecutive pixels, such an edge is called a ramp. The edge highlight filter works by recognizing sharp edges in the image (for example, the edge between the subject and the background) and increasing the contrast of the image in the area directly around the edge. This makes the edge look more defined. The image below shows an example of highlighting edges:Input image Output image 
We use a 3x3 Laplace core for the edge highlighting process. We multiply each pixel and its surroundings in the original image by the Laplace core, add the products, and use the sum for the value of the pixel in the new image with the highlighted edges. We call this process convolution. The figure below shows one step of the convolution with the Laplace nucleus.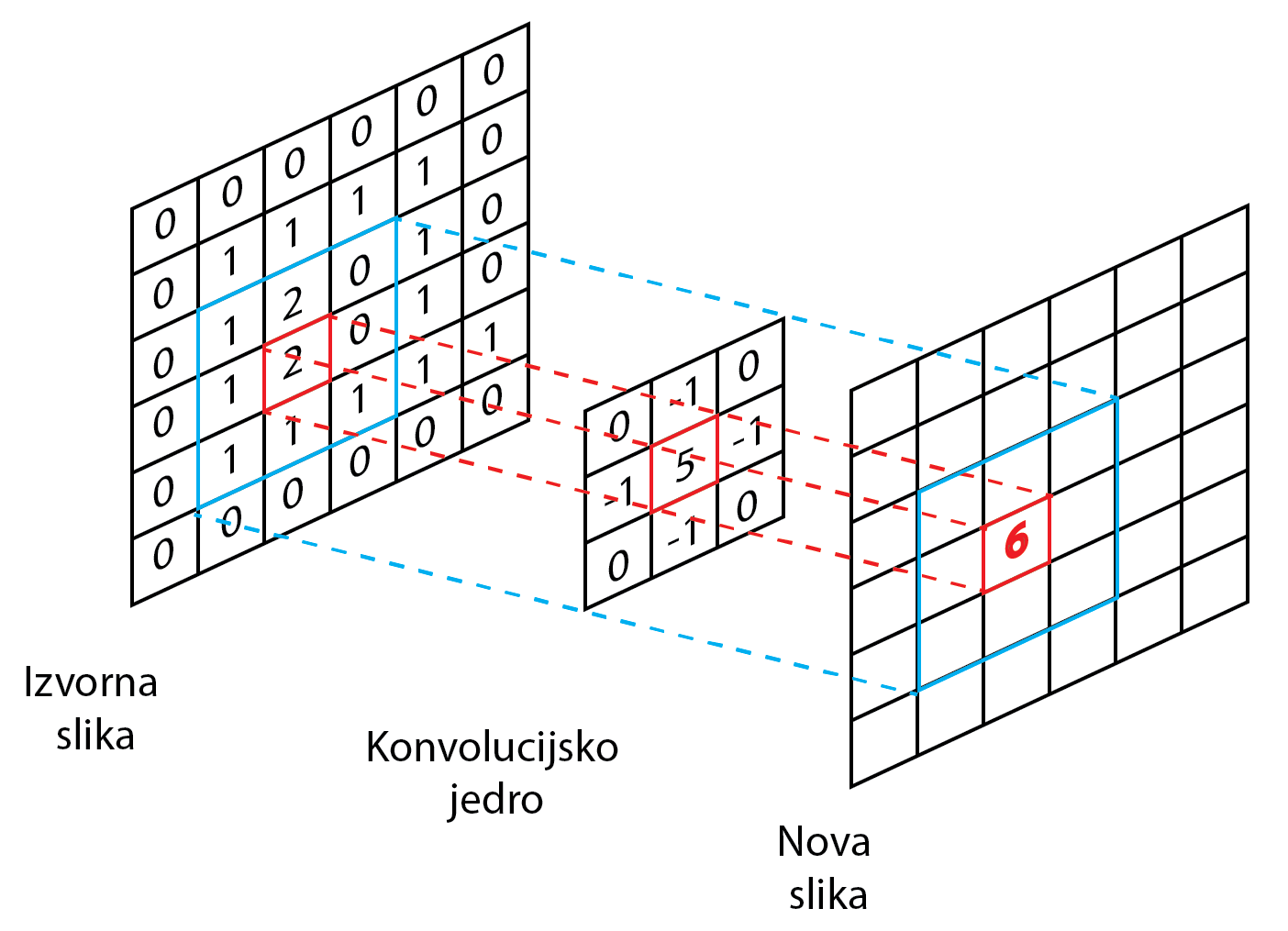
The figure shows the Lapac core, which we will use to highlight the edges in the figure. We see how we emphasize the value of the pixel with a value of 2, which forms an edge with a pixel on its right (value 0). The new value, 6, is obtained by placing the core on the original image, multiplying the identical elements and adding the partial products.Working with pictures
We will use the publicly accessible STB library to read images from disk to memory and write back to disk. The library is quite extensive, but we will only use the stbi_load and stbi_write functions, which are defined in the stb_image.h and stb_image_write.h headers. Instructions for using the functions can be found here.Images in memory
We will first read the images from the files on the disk into memory. Images are made up of a multitude of pixels. For grayscale images, one pixel is usually represented by eight bits that define the grayscale level (from black to white). The image plane of the Width x Height dimension is represented in the memory as a vector of image points, whereby an individual image point is accessed as follows: image [Y x Width + X]. Access to each image point is shown in the image below.
The quantities X (column), Y (row), Width (width) and Height (height) are expressed in pixels.
For color images, typically each pixel is represented by 4 x 8 bits or four bytes. The first three bytes specify the three color components (RGB, Red, Green, and Blue), while for certain records (such as png), the last byte specifies transparency. We also say that an image consists of four channels. Each pixel is therefore represented in memory by four values, each value being written by one byte. The four-channel image of the Width x Height dimensions in memory is shown in the image below.
An individual pixel is now accessed as follows: image [(Y x Width + X) x CPP + channel], where CPP is the number of channels per pixel and can be between 1 and 4, channel however, the channel index is from 0 to 3.
In the following, we will limit ourselves to four-channel images (even if they are gray) and we will write them to memory with the stbi_load function. In the case of grayscale images (Rn channel), the last three bytes of the pixel will be unused. At first glance, the solution is wasteful, as grayscale images take up four times as much memory space, but we will have the same code to process all types of images because of this.Kernels to emphasize the edges
Each thread will calculate a new value of one pixel in the image. For this purpose, with 3x3 filters, it will have to access eight more pixels in the immediate vicinity of the pixel for which it calculates the new value. With a selected Laplace kernel, it is sufficient to access only four adjacent pixels at which the kernel has nonzero values.
In the following, we present four kernels - from the most inefficient and at the same time the simplest to the most efficient and the most complex.Naive filter for powdering edges
The simplest implementation of a sharpenGPU kernel to use an edge highlight filter is shown in the code below.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
//Simplest kernel (memory accesses not optimal) __kernel void sharpenGPU(__global unsigned char *imageIn, __global unsigned char *imageOut, int width, int height, int cpp) { int y = get_global_id(0); int x = get_global_id(1); if (x < width && y < height) { // for each color channel for (int c = 0; c < cpp; c++) { unsigned char px01 = getIntensity(imageIn, y - 1, x, c, height, width, cpp); unsigned char px10 = getIntensity(imageIn, y, x - 1, c, height, width, cpp); unsigned char px11 = getIntensity(imageIn, y, x, c, height, width, cpp); unsigned char px12 = getIntensity(imageIn, y, x + 1, c, height, width, cpp); unsigned char px21 = getIntensity(imageIn, y + 1, x, c, height, width, cpp); short pxOut = (5 * px11 - px01 - px10 - px12 - px21); if (pxOut > 255) pxOut = 255; if (pxOut < 0) pxOut = 0; imageOut[(y * width + x) * cpp + c] = (unsigned char)pxOut; } } }In the for loop, we walk across all the channels and for each channel separately, the thread reads the values of five pixels from the image: the pixel for which it calculates the new value, and its four neighbors (left, right, top and bottom), as required by the Laplace core . To access the values of individual pixels, prepare the getIntensity function:
1 2 3 4 5 6 7 8 9 10 11 12
//Helper function to extract intensity value for a pixel form image inline unsigned char getIntensity( __global unsigned char *image, int y, int x, int channel, int height, int width, int cpp) { if (x < 0 || x >= width) return 0; if (y < 0 || y >= height) return 0; return image[(y * width + x) * cpp + channel]; }Such a kernel is simple, but it has one serious drawback. As we have written many times, access to main memory is always done by all threads from the bundle at the same time and is always 128 bytes long - four bytes per thread. In our case, each thread needs only one of four bytes in one iteration, but reads all four when reading and discards unnecessary ones! Then in the next iteration it accesses the same segment in the global memory again, even though it accessed this segment in the previous iteration! But what if, in the previous iteration, she simply discarded the data she didn’t need at the time.The two-dimensional space of NDRange is set as follows:1 2 3 4 5
const size_t szLocalWorkSize[2] = {16, 16}; const size_t szGlobalWorkSize[2] = { ((width - 1) / szLocalWorkSize[1] + 1) * szLocalWorkSize[1], ((height - 1) / szLocalWorkSize[0] + 1) * szLocalWorkSize[0] };Threads will be implemented in 16 x 16 workgroups. The total number of threads (global size of the NDRange space) depends on the size of the input image and must be divisible by the size of the workgroup in both dimensions, in our case 16. Because the dimensions of the input images are not necessarily divisible by 16, when determining the number of threads, round the size of the image upwards so that it is divisible by 16.A kernel of sharpenGPU is performed in 1.39 milliseconds on an Nvidia Tesla K40 GPE when processing an image of 2580x1319 pixels:[patriciob@nsc-login 09-image-filter]$ srun prog sharpenGPU celada_in.png celada_out.png Loaded image celada_in.png of size 2580x1319. Program size = 5894 B Kernel Execution time is: 1.388 millisecondsEdge highlighting filter with regard to the organization of data in memory
A more efficient kernel is obtained by considering the mechanism of access to global memory (memory coalescing). The thread in the bundle always has access to at least four bytes, so it's a good idea to take advantage of this - read all four channels with one read! We use OpenCL vector data types for this purpose. Vector data types allow us to perform operations on short vectors of length 2, 4, 8 or 16 elements. The arithmetic operation is performed simultaneously over the parallel elements of the vectors. The code below shows a kernel of sharpenGPU_vector, which reads all four channels into a vector of length four at a time and performs the operation required by the Laplace kernel over all elements of the vector (all channels) at once.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
__kernel void sharpenGPU_vector(__global uchar4 *imageIn, __global uchar4 *imageOut, int width, int height) { int y = get_global_id(1); int x = get_global_id(0); if (x < width && y < height) { short4 px01 = getIntensity4(imageIn, y - 1, x, height, width); short4 px10 = getIntensity4(imageIn, y, x - 1, height, width); short4 px11 = getIntensity4(imageIn, y, x, height, width); short4 px12 = getIntensity4(imageIn, y, x + 1, height, width); short4 px21 = getIntensity4(imageIn, y + 1, x, height, width); short4 pxOut = (short4)(5) * px11 - px01 - px10 - px12 - px21; imageOut[y * width + x] = convert_uchar4_sat(pxOut); } }The uchar4-type kernel arguments are vectors containing four 8-bit values (uchar type). Similarly, short4 is a vector of four 16-bit short data. The openCL function convert_uchar4_sat (line 17) explicitly converts the vector of 16-bit short4 elements into the vector of 8-bit uchar4 elements using saturation arithmetic. To vector read individual pixels from global memory, use the getIntensity4 function:1 2 3 4 5 6 7 8 9
inline short4 getIntensity4(__global uchar4 *image, int y, int x, int height, int width) { if (x < 0 || x >= width) return (short4)(0); if (y < 0 || y >= height) return (short4)(0); return convert_short4(image[y * width + x]); }The openCL function convert_short4 performs an explicit conversion from the uchar4 vector to the short4 vector. This time, a kernel of sharpenGPU_vecotor on the Nvidia Tesla K40 GPE is performed in 0.66 milliseconds when processing an image of 2580x1319 pixels:
[patriciob@nsc-login 09-image-filter]$ srun prog sharpenGPU_vector celada_in.png celada_out.png Loaded image celada_in.png of size 2580x1319. Program size = 5894 B Kernel Execution time is: 0.662 millisecondsWe see that the acceleration due to the consideration of global memory accesses is considerable and therefore we must always be careful how the threads access the data in the global memory.Edge highlighting filter using local memory
In the previous kernels, each thread reads five pixels. Since each pixel in the image is adjacent to four pixels (left, right, top, and bottom), we will read each pixel from main memory four times. 256 threads in a 16x16 workgroup practically share adjacent pixels. Therefore, it is better to read a sub-image of the appropriate size from the image in the global memory to the local memory. This way, the threads in the workgroup will have all the necessary pixels in the local memory. Access to pixel data will be several hundred times faster, and we will read each pixel only once from global memory. In fact, we need to read 18x18 pixels into the local memory, because even at the edges of the workgroup they need an extra edge of pixels.The sharpenGPU_local_vector pin to highlight edges using local memory is represented by the code below.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
__kernel void sharpenGPU_local_vector_linear(__global uchar4 *imageIn, __global uchar4 *imageOut, int width, int height, int cpp) { int gy = get_global_id(1); int gx = get_global_id(0); int ly = get_local_id(1); int lx = get_local_id(0); int lsy=get_local_size(1); int lsx=get_local_size(0); // reserve local memory __local short4 imgChunk[CHUNK_SIZE * CHUNK_SIZE]; // load an image chunk to local memory // linearize local indices and move block through the image chunk for (int lli=ly*lsx+lx;lli<CHUNK_SIZE*CHUNK_SIZE;lli+=lsx*lsy){ int groupx=get_group_id(0)*lsx; // global X offset for the work-group int groupy=get_group_id(1)*lsy; // global Y offset for the work-group // Now calculate 2D global indices back from local linear ones: int gyi=groupy+(lli/CHUNK_SIZE)-1; // ROW: global Y offset + row in the workgroup int gxi=groupx+lli%CHUNK_SIZE-1; // COLUMN: global X offset + column in the workgroup // read pixel flom global to local memory imgChunk[lli]=getIntensity4(imageIn, gyi, gxi, height, width, cpp); } // wait for threads to finish barrier(CLK_LOCAL_MEM_FENCE); if (gx < width && gy < height) { int pxi = (ly + 1) * CHUNK_SIZE + (lx + 1); short4 px01 = imgChunk[pxi - CHUNK_SIZE]; short4 px10 = imgChunk[pxi - 1]; short4 px11 = imgChunk[pxi]; short4 px12 = imgChunk[pxi + 1]; short4 px21 = imgChunk[pxi + CHUNK_SIZE]; short4 pxOut = (short4)(5) * px11 - px01 - px10 - px12 - px21; imageOut[gy * width + gx] = convert_uchar4_sat(pxOut); } }First, the threads transfer a chunk of image from the global memory to the local memory (lines 19-32).Assume that CHUNK_SIZE = 4 and that the size of the workgroups is 2x2 (get_local_size() returns 2 in both dimensions). This means that 4 threads must transfer 16 elements from the global memory to imgChunk in the local memory. Note that imgChunk is declared as a 1D vector (line 12 in a kernel of sharpenGPU_local_vector) and not as a 2D box! Nor do they transfer data from global memory to local memory, as shown in the figure below:
To have access to consecutive words in global memory, for one block of thread we always calculate all the linearized indices (lli) of the elements in imgChunk that the individual threads in the block carry. These linearized indexes are also used to determine the global memory elements that each thread transmits (picture on the right) with the following code:
25 26 27
// Now calculate 2D global indices back from local linear ones: int gyi=groupy+(lli/CHUNK_SIZE)-1; // ROW: global Y offset + row in the workgroup int gxi=groupx+lli%CHUNK_SIZE-1; // COLUMN: global X offset + column in the workgroupwhere groupx and groupy determine the global offset of the workgroup in global memory.Before calculating the output image point, all threads wait at the obstacle. Each thread then calculates a new value for its pixel, reading the sub-image from local memory (imgChunk):34 35 36 37 38 39 40 41 42 43 44 45 46 47
// wait for threads to finish barrier(CLK_LOCAL_MEM_FENCE); if (gx < width && gy < height) { int pxi = (ly + 1) * CHUNK_SIZE + (lx + 1); short4 px01 = imgChunk[pxi - CHUNK_SIZE]; short4 px10 = imgChunk[pxi - 1]; short4 px11 = imgChunk[pxi]; short4 px12 = imgChunk[pxi + 1]; short4 px21 = imgChunk[pxi + CHUNK_SIZE]; short4 pxOut = (short4)(5) * px11 - px01 - px10 - px12 - px21; imageOut[gy * width + gx] = convert_uchar4_sat(pxOut); }This time kernel of sharpenGPU_local_vector on the Nvidia Tesla K40 GPE is performed in 0.56 milliseconds when processing a 2580x1319 pixel image:
[patriciob@nsc-login 09-image-filter]$ srun prog sharpenGPU_local_vector_linear celada_in.png celada_out.png Loaded image celada_in.png of size 2580x1319. Program size = 7000 B Kernel Execution time is: 0.557 millisecondsWe see that the use of local memory brings us additional performance speed, as each image element is read only once from the global memory (except for image elements at the edges, which are read twice). Compared to the naive version of the kernel, the acceleration is 2.5 times! The latter finding should not surprise us, as we know that the bottleneck in computers is actually DRAM memory, and by considering the organization of data in DRAM memory, how to access DRAM memory, and caching (since local memory is a software-controlled cache), we can significantly influence time implementation of the programs.
The full code from this chapter can be found in the 09-image-filter folder here.
-